
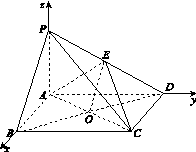
如图13,四棱锥PABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(1)证明:PB∥平面AEC;
(2)设二面角DAEC为60°,AP=1,AD= ,求三棱锥EACD的体积.
,求三棱锥EACD的体积.
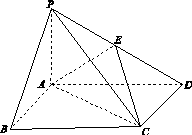
图13
解:(1)证明:连接BD交AC于点O,连接EO.
因为ABCD为矩形,所以O为BD的中点.
又E为PD的中点,所以EO∥PB.
因为EO⊂平面AEC,PB⊄平面AEC,
所以PB∥平面AEC.
(2)因为PA⊥平面ABCD,ABCD为矩形,
所以AB,AD,AP两两垂直.
如图,以A为坐标原点, ,AD,AP的方向为x轴、y轴、z轴的正方向,|
,AD,AP的方向为x轴、y轴、z轴的正方向,| |为单位长,建立空间直角坐标系Axyz,则D
|为单位长,建立空间直角坐标系Axyz,则D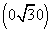 ,E
,E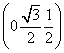 ,
,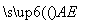 =
=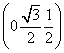 .
.
设B(m,0,0)(m>0),则C(m, ,0),
,0),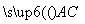 =(m,
=(m, ,0).
,0).
设n1=(x,y,z)为平面ACE的法向量,
则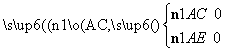 即
即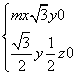
可取n1=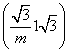 .
.
又n2=(1,0,0)为平面DAE的法向量,
由题设易知|cos〈n1,n2〉|= ,即
,即
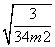 =
= ,解得m=
,解得m=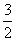 .
.
因为E为PD的中点,所以三棱锥EACD的高为 .三棱锥EACD的体积V=
.三棱锥EACD的体积V=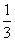 ×
× ×
× ×
×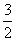 ×
× =
=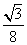 .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
设集合A={1,2},B={1,2,3},分别从集合A和B中随机取一个数a和b,确定平面上的一个点P(a,b),记“点P(a,b)落在直线x+y=n上”为事件Cn(2≤n≤5,n∈N),若事件Cn的概率最大,则n的所有可能值为( )
A.3 B.4
C.2和5 D.3和4
查看答案和解析>>
科目:高中数学 来源: 题型:
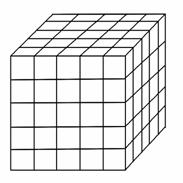
.如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体.经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=( )
A.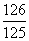 B.
B.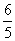
C.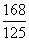 D.
D.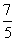
查看答案和解析>>
科目:高中数学 来源: 题型:
几何体的三视图(单位:cm)如图11所示,则此几何体的表面积是( )
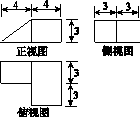
图11
A.90 cm2 B.129 cm2 C.132 cm2 D.138 cm2
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD.将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图15所示.
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
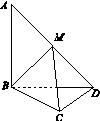
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
如图16,四棱锥P ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
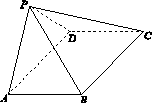
图16
(1)求证:AB⊥PD.
(2)若∠BPC=90°,PB= ,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
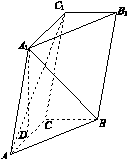
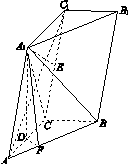
如图11所示,三棱柱ABC A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面BCC1B1的距离为 ,求二面角A1 AB C的大小.
,求二面角A1 AB C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知二面角αlβ为60°,AB⊂α,AB⊥l,A为垂足,CD⊂β,C∈l,∠ACD=135°,则异面直线AB与CD所成角的余弦值为( )
A.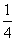 B.
B.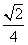
C.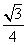 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
现有编号分别为1,2,3,4,5的五道不同的政治题和编号分别为6,7,8,9的四道不同的历史题.甲同学从这九道题中一次性随机抽取两道题,每道题被抽到的概率是相等的,用符号(x,y)表示事件“抽到的两道题的编号分别为x、y,且x<y”.
(1)问有多少个基本事件,并列举出来;
(2)求甲同学所抽取的两道题的编号之和小于17但不小于11的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com