
如图16,四棱锥P ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
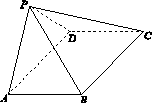
图16
(1)求证:AB⊥PD.
(2)若∠BPC=90°,PB= ,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
解:(1)证明:因为ABCD为矩形,所以AB⊥AD.
又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,
所以AB⊥平面PAD,故AB⊥PD.
(2)过P作AD的垂线,垂足为O,过O作BC的垂线,垂足为G,连接PG.
故PO⊥平面ABCD,BC⊥平面POG,BC⊥PG.
在Rt△BPC中,PG=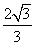 ,GC=
,GC=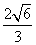 ,BG=
,BG=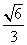 .
.
设AB=m,则OP=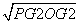 =
=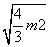 ,故四棱锥P ABCD的体积为
,故四棱锥P ABCD的体积为
V=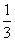 ×
×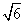 ·m·
·m·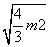 =
=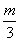
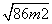 .
.
因为m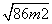 =
=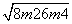 =
=
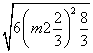 ,
,
所以当m=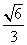 ,即AB=
,即AB=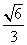 时,四棱锥P ABCD的体积最大.
时,四棱锥P ABCD的体积最大.
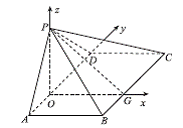
此时,建立如图所示的空间直角坐标系,各点的坐标分别为O(0,0,0),B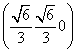 ,C
,C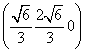 ,D
,D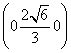 ,P
,P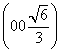 ,故
,故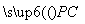 =
=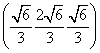 ,
,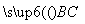 =(0,
=(0,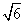 ,0),CD=
,0),CD=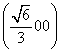 .
.
设平面BPC的一个法向量为n1=(x,y,1),
则由n1⊥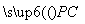 ,n1⊥
,n1⊥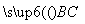 ,得
,得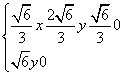 解得x=1,y=0,则n1=(1,0,1).
解得x=1,y=0,则n1=(1,0,1).
同理可求出平面DPC的一个法向量为n2=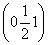 .
.
设平面BPC与平面DPC的夹角为θ,则cos θ=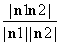 =
=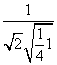 =
=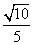 .
.


科目:高中数学 来源: 题型:
设连续掷两次骰子得到的点数分别为m,n,令平面向量a=(m,n),b=(1,-3).
(1)求使得事件“a⊥b”发生的概率;
(2)求使得事件“|a|≤|b|”发生的概率;
(3)求使得事件“直线y=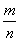 x与圆(x-3)2+y2=1相交”发生的概率.
x与圆(x-3)2+y2=1相交”发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
袋中有20个大小相同的球,其中记上0号的有10个,记上n号的有n个(n=1,2,3,4),现从袋中任取一球,ξ表示所取球的标号.
(1)求ξ的分布列、期望和方差;
(2)若η=aξ+b,E(η)=1,D(η)=11,试求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图13,四棱锥PABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(1)证明:PB∥平面AEC;
(2)设二面角DAEC为60°,AP=1,AD= ,求三棱锥EACD的体积.
,求三棱锥EACD的体积.
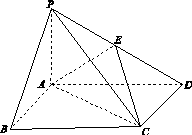
图13
查看答案和解析>>
科目:高中数学 来源: 题型:
如图15,在四棱锥A BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= .
.
(1)证明:DE⊥平面ACD;
(2)求二面角B AD E的大小.
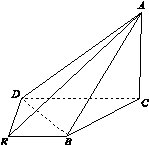
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
如图14所示,在四棱锥P ABCD中,PA⊥底面ABCD, AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F AB P的余弦值.
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
某射手射击所得环数X的分布列为:
| X | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| P | 0.02 | 0.04 | 0.06 | 0.09 | 0.28 | 0.29 | 0.22 |
则此射手“射击一次命中环数大于7”的概率为( )
A.0.28 B.0.88
C.0.79 D.0.51
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com