练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某射手射击所得环数X的分布列为：

    X

    4

    5

    6

    7

    8

    9

    10

    P

    0.02

    0.04

    0.06

    0.09

    0.28

    0.29

    0.22

    则此射手“射击一次命中环数大于7”的概率为(　　)

    A．0.28                                 B．0.88

    C．0.79                                 D．0.51


    C


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     如图1­6，四棱锥P ­ ABCD中，ABCD为矩形，平面PAD⊥平面ABCD.

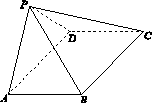
    图1­6

    (1)求证：AB⊥PD.

    (2)若∠BPC＝90°，PB＝，PC＝2，问AB为何值时，四棱锥P ­ ABCD的体积最大？并求此时平面BPC与平面DPC夹角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在三棱柱ABC­A1B1C1中，侧面ABB1A1为矩形，AB＝1，AA1＝，D为AA1的中点，BD与AB1交于点O，CO⊥侧面ABB1A1.

    (1)证明：BC⊥AB1；

    (2)若OC＝OA，求直线C1D与平面ABC所成角的正弦值．

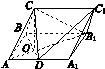
    图J12­2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    投掷两颗骰子，得到其向上的点数分别为m和n，则复数(m＋ni)(n－mi)为实数的概率为(　　)

    A.                                    B.

    C.                                    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    现有编号分别为1,2,3,4,5的五道不同的政治题和编号分别为6,7,8,9的四道不同的历史题．甲同学从这九道题中一次性随机抽取两道题，每道题被抽到的概率是相等的，用符号(x，y)表示事件“抽到的两道题的编号分别为x、y，且x<y”．

    (1)问有多少个基本事件，并列举出来；

    (2)求甲同学所抽取的两道题的编号之和小于17但不小于11的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知随机变量ξ只能取三个值：x1，x2，x3，其概率依次成等差数列，则公差d的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一个均匀的正四面体的四个面上分别标有1,2,3,4四个数字，现随机投掷两次，正四面体面朝下的数字分别为x1，x2，记ξ＝(x1－3)2＋(x2－3)2.

    (1)分别求出ξ取得最大值和最小值时的概率．

    (2)求ξ的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示的几何体中，四边形ABCD为矩形，AD⊥平面，AE=EB=BC=2，F为CE上的点，且BF⊥平面ACE．

    （1）求证：AE∥平面BFD；

    （2）求三棱锥C﹣BGF的体积．

    　

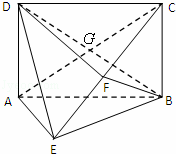
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝x2＋2ax＋3，x∈[－4,6]．

    (1)当a＝－2时，求f(x)的最值；

    (2)求实数a的取值范围，使y＝f(x)在区间[－4,6]上是单调函数。

    查看答案和解析>>

    同步练习册答案