练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

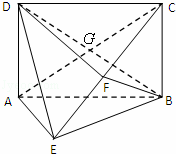
    如图所示的几何体中，四边形ABCD为矩形，AD⊥平面，AE=EB=BC=2，F为CE上的点，且BF⊥平面ACE．

    （1）求证：AE∥平面BFD；

    （2）求三棱锥C﹣BGF的体积．

    　


    解答： （1）证明：如图，

    由题意可得G是AC的中点，连接FG，

    ∵BF⊥平面ACE，则CE⊥BF，而BC=BE，

    ∴F是EC中点，

    在△AEC中，FG∥AE，∴AE∥平面BFD；

    （2）解：∵AE∥平面BFD，∴AE∥FG，

    由题可得AE⊥平面BCE，∴FG⊥平面BCE．

    ∵G是AC的中点，F是CE中点，∴AE∥FG且FG=，

    ∵BF⊥平面ACE，∴BF⊥CE，∴Rt△BCE中，BF=，

    ∴，

    ∴=．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图1­4所示，在四棱锥P ­ ABCD中，PA⊥底面ABCD,  AD⊥AB，AB∥DC，AD＝DC＝AP＝2，AB＝1，点E为棱PC的中点．

    (1)证明：BE⊥DC；

    (2)求直线BE与平面PBD所成角的正弦值；

    (3)若F为棱PC上一点，满足BF⊥AC，求二面角F ­ AB ­ P的余弦值．

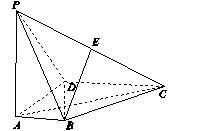
    图1­4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某射手射击所得环数X的分布列为：

    X

    4

    5

    6

    7

    8

    9

    10

    P

    0.02

    0.04

    0.06

    0.09

    0.28

    0.29

    0.22

    则此射手“射击一次命中环数大于7”的概率为(　　)

    A．0.28                                 B．0.88

    C．0.79                                 D．0.51

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若α，β是两个不同的平面，下列四个条件：

    ①存在一条直线a，a⊥α，a⊥β；

    ②存在一个平面γ，γ⊥α，γ⊥β；

    ③存在两条平行直线a，b，a⊂α，b⊂β，a∥β，b∥α；

    ④存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α．

    那么可以是α∥β的充分条件有（　C　）

    　 A． 4个 B． 3个 C． 2个 D． 1个

    　

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知双曲线的方程为﹣x2=1，点A的坐标为（0，﹣），B是圆（x﹣）2+y2=1上的点，点M在双曲线的上支上，则|MA|+|MB|的最小值为　　　　　　．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若A（﹣2，3）、B（3，﹣2）、C（，m﹚三点在同一直线上，则m的值为（　　）

    　 A． ﹣2 B． 2 C． ﹣ D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    三个球的半径之比是1：2：3　则最大球的体积是其余两个球的体积之和的（　　）

    　 A． 4倍 B． 3倍 C． 2倍 D． 1倍

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a＝log36，b＝log510，c＝log714，则(　　)

    A. c>b>a       B. b>c>a         C. a>c>b            D. a>b>c

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝()x－log2(x＋2)在区间[－1，1]上的最大值为(　　)

    A．1  B．3  C．4  D．5

    查看答案和解析>>

    同步练习册答案