
在三棱柱ABCA1B1C1中,侧面ABB1A1为矩形,AB=1,AA1= ,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
(1)证明:BC⊥AB1;
(2)若OC=OA,求直线C1D与平面ABC所成角的正弦值.
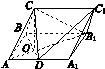
图J122
解:(1)证明:由题意可知,在Rt△ABD中,tan∠ABD=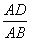 =
=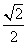 ,在Rt△ABB1中,tan∠AB1B=
,在Rt△ABB1中,tan∠AB1B=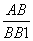 =
=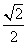 .
.
又因为0<∠ABD,∠AB1B<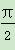 ,所以∠ABD=∠AB1B,
,所以∠ABD=∠AB1B,
所以∠ABD+∠BAB1=∠AB1B+∠BAB1=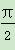 ,
,
所以AB1⊥BD.
又CO⊥侧面ABB1A1,且AB1⊂侧面ABB1A1,∴AB1⊥CO.
又BD与CO交于点O,所以AB1⊥平面CBD.
又因为BC⊂平面CBD,所以BC⊥AB1.
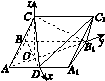
(2)如图所示,分别以OD,OB1,OC所在的直线为x轴,y轴,z轴,以O为原点,建立空间直角坐标系,
则A0,-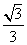 ,0,B-
,0,B-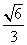 ,0,0,C0,0,
,0,0,C0,0,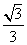 ,B10,
,B10,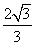 ,0,D
,0,D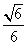 ,0,0.
,0,0.



 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
袋中有20个大小相同的球,其中记上0号的有10个,记上n号的有n个(n=1,2,3,4),现从袋中任取一球,ξ表示所取球的标号.
(1)求ξ的分布列、期望和方差;
(2)若η=aξ+b,E(η)=1,D(η)=11,试求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图14所示,在四棱锥P ABCD中,PA⊥底面ABCD, AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F AB P的余弦值.
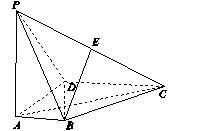
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
把边长为 的正方形ABCD沿对角线BD折起,连接AC,得到三棱锥C ABD,其正视图、俯视图为全等的等腰直角三角形(如图X243所示),则其侧视图的面积为( )
的正方形ABCD沿对角线BD折起,连接AC,得到三棱锥C ABD,其正视图、俯视图为全等的等腰直角三角形(如图X243所示),则其侧视图的面积为( )
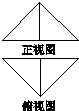
图X243
A. B.
B. C.1 D.
C.1 D.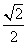
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙两人一起到阿里山参观旅游,他们约定,各自独立地从1到6号景点中任选4个进行游览,每个景点参观1小时,则最后1小时他们同在一个景点的概率是( )
A.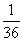 B.
B.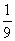
C.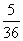 D.
D.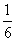
查看答案和解析>>
科目:高中数学 来源: 题型:
某学院为了调查本校学生2014年9月“健康上网”(健康上网是指每天上网不超过两个小时)的天数情况,随机抽取了40名本校学生作为样本,统计他们在该月30天内健康上网的天数,并将所得的数据分成以下六组:[0,5],(5,10],(10,15],…,(25,30],由此画出样本的频率分布直方图,如图所示.
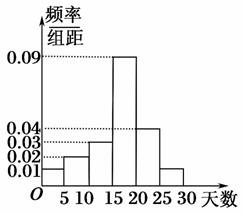
(1)根据频率分布直方图,求这40名学生中健康上网天数超过20天的人数;
(2)现从这40名学生中任取2名,设Y为取出的2名学生中健康上网天数超过20天的人数,求Y的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
某射手射击所得环数X的分布列为:
| X | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| P | 0.02 | 0.04 | 0.06 | 0.09 | 0.28 | 0.29 | 0.22 |
则此射手“射击一次命中环数大于7”的概率为( )
A.0.28 B.0.88
C.0.79 D.0.51
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com