
把边长为 的正方形ABCD沿对角线BD折起,连接AC,得到三棱锥C ABD,其正视图、俯视图为全等的等腰直角三角形(如图X243所示),则其侧视图的面积为( )
的正方形ABCD沿对角线BD折起,连接AC,得到三棱锥C ABD,其正视图、俯视图为全等的等腰直角三角形(如图X243所示),则其侧视图的面积为( )
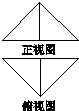
图X243
A. B.
B. C.1 D.
C.1 D.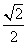
 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
.如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体.经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=( )
A.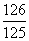 B.
B.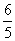
C.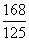 D.
D.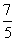
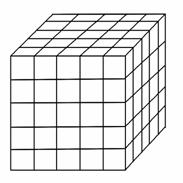
查看答案和解析>>
科目:高中数学 来源: 题型:
如图11所示,三棱柱ABC A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面BCC1B1的距离为 ,求二面角A1 AB C的大小.
,求二面角A1 AB C的大小.
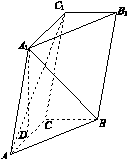
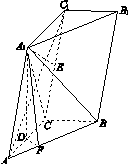
查看答案和解析>>
科目:高中数学 来源: 题型:
已知二面角αlβ为60°,AB⊂α,AB⊥l,A为垂足,CD⊂β,C∈l,∠ACD=135°,则异面直线AB与CD所成角的余弦值为( )
A.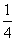 B.
B.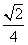
C.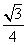 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图15,在四棱锥A BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= .
.
(1)证明:DE⊥平面ACD;
(2)求二面角B AD E的大小.
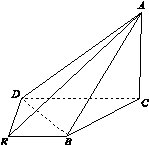
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
在三棱柱ABCA1B1C1中,侧面ABB1A1为矩形,AB=1,AA1= ,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
(1)证明:BC⊥AB1;
(2)若OC=OA,求直线C1D与平面ABC所成角的正弦值.
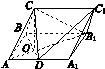
图J122
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙、丙3位教师安排在周一至周五中的3天值班,要求每人值班1天且每天至多安排1人,则恰好甲安排在另外两位教师前面值班的概率是( )
A.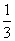 B.
B. C.
C.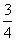 D.
D.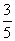
查看答案和解析>>
科目:高中数学 来源: 题型:
现有编号分别为1,2,3,4,5的五道不同的政治题和编号分别为6,7,8,9的四道不同的历史题.甲同学从这九道题中一次性随机抽取两道题,每道题被抽到的概率是相等的,用符号(x,y)表示事件“抽到的两道题的编号分别为x、y,且x<y”.
(1)问有多少个基本事件,并列举出来;
(2)求甲同学所抽取的两道题的编号之和小于17但不小于11的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com