
已知二面角αlβ为60°,AB⊂α,AB⊥l,A为垂足,CD⊂β,C∈l,∠ACD=135°,则异面直线AB与CD所成角的余弦值为( )
A.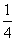 B.
B.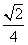
C.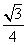 D.
D.
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
如图,用K,A1,A2三类不同的元件连接成一个系统.当K正常工作且A1,A2至少有一个正常工作时,系统正常工作.已知K,A1,A2正常工作的概率依次为0.9、0.8、0.8,则系统正常工作的概率为( )
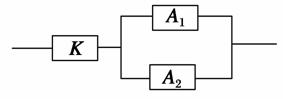
A.0.960 B.0.864
C.0.720 D.0.576
查看答案和解析>>
科目:高中数学 来源: 题型:
如图13,四棱锥PABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(1)证明:PB∥平面AEC;
(2)设二面角DAEC为60°,AP=1,AD= ,求三棱锥EACD的体积.
,求三棱锥EACD的体积.
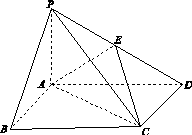
图13
查看答案和解析>>
科目:高中数学 来源: 题型:
如图13,正方形AMDE的边长为2,B,C分别为AM,MD的中点.在五棱锥P ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.
(1)求证:AB∥FG;
(2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长.
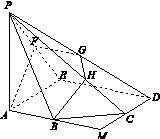
图13
查看答案和解析>>
科目:高中数学 来源: 题型:
如图14所示,在四棱锥P ABCD中,PA⊥底面ABCD, AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F AB P的余弦值.
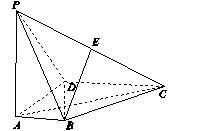
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
把边长为 的正方形ABCD沿对角线BD折起,连接AC,得到三棱锥C ABD,其正视图、俯视图为全等的等腰直角三角形(如图X243所示),则其侧视图的面积为( )
的正方形ABCD沿对角线BD折起,连接AC,得到三棱锥C ABD,其正视图、俯视图为全等的等腰直角三角形(如图X243所示),则其侧视图的面积为( )
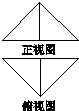
图X243
A. B.
B. C.1 D.
C.1 D.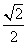
查看答案和解析>>
科目:高中数学 来源: 题型:
某学院为了调查本校学生2014年9月“健康上网”(健康上网是指每天上网不超过两个小时)的天数情况,随机抽取了40名本校学生作为样本,统计他们在该月30天内健康上网的天数,并将所得的数据分成以下六组:[0,5],(5,10],(10,15],…,(25,30],由此画出样本的频率分布直方图,如图所示.
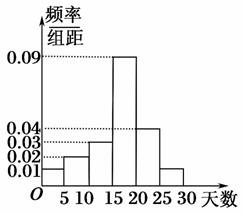
(1)根据频率分布直方图,求这40名学生中健康上网天数超过20天的人数;
(2)现从这40名学生中任取2名,设Y为取出的2名学生中健康上网天数超过20天的人数,求Y的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com