
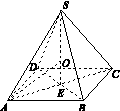
正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A. B.16π C.9π D.
B.16π C.9π D.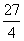
科目:高中数学 来源: 题型:
某幼儿园在“六·一儿童节”开展了一次亲子活动,此次活动由宝宝和父母之一(后面以家长代称)共同完成,幼儿园提供了两种游戏方案:
方案一:宝宝和家长同时各抛掷一枚质地均匀的正方体骰子(六个面的点数分别是1,2,3,4,5,6),宝宝所得点数记为x,家长所得点数记为y;
方案二:宝宝和家长同时按下自己手中一个计算器的按钮(此计算器只能产生区间[1,6]的随机实数),宝宝的计算器产生的随机实数记为m,家长的计算器产生的随机实数记为n.
(1)在方案一中,若x+1=2y,则奖励宝宝一朵小红花,求抛掷一次后宝宝得到一朵小红花的概率;
(2)在方案二中,若m>2n,则奖励宝宝一本兴趣读物,求按下一次按钮后宝宝得到一本兴趣读物的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
几何体的三视图(单位:cm)如图11所示,则此几何体的表面积是( )
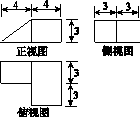
图11
A.90 cm2 B.129 cm2 C.132 cm2 D.138 cm2
查看答案和解析>>
科目:高中数学 来源: 题型:
如图16,四棱锥P ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
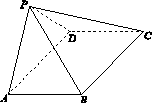
图16
(1)求证:AB⊥PD.
(2)若∠BPC=90°,PB= ,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
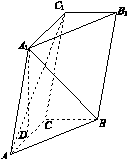
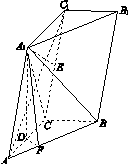
如图11所示,三棱柱ABC A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面BCC1B1的距离为 ,求二面角A1 AB C的大小.
,求二面角A1 AB C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图14,在棱长为2的正方体ABCDA1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1,A1D1的中点,点P,Q分别在棱DD1,BB1上移动,且DP=BQ=λ(0<λ<2).
(1)当λ=1时,证明:直线BC1∥平面EFPQ.
(2)是否存在λ,使面EFPQ与面PQMN所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.
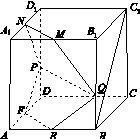
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
已知二面角αlβ为60°,AB⊂α,AB⊥l,A为垂足,CD⊂β,C∈l,∠ACD=135°,则异面直线AB与CD所成角的余弦值为( )
A.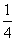 B.
B.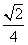
C.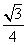 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
在三棱柱ABCA1B1C1中,侧面ABB1A1为矩形,AB=1,AA1= ,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
(1)证明:BC⊥AB1;
(2)若OC=OA,求直线C1D与平面ABC所成角的正弦值.
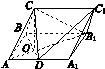
图J122
查看答案和解析>>
科目:高中数学 来源: 题型:
一个均匀的正四面体的四个面上分别标有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为x1,x2,记ξ=(x1-3)2+(x2-3)2.
(1)分别求出ξ取得最大值和最小值时的概率.
(2)求ξ的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com