
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按150进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失)得到的频率分布表如下:
| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 合计 |
| 频数 |
|
|
| b | ||
| 频率 | a | 0.25 |
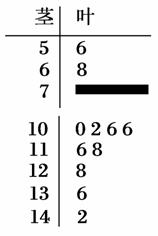
(1)求表中a,b的值及分数在[90,100)范围内的学生人数,并估计这次考试全校学生数学成绩及格率(分数在[90,150]范围为及格).
(2)从大于等于110分的学生中随机选2名学生得分,求2名学生的平均得分大于等于130分的概率.
解 (1)由茎叶图可知分数在[50,70)范围内的有2人,在[110,130)范围内的有3人,所以a=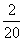 =0.1,b=3.
=0.1,b=3.
又分数在[110,150)范围内的频率为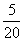 =0.25,
=0.25,
所以分数在[90,110)范围内的频率为1-0.1-0.25-0.25=0.4,所以分数在[90,110)范围内的人数为20×0.4=8,
由茎叶图可知分数在[100,110)范围内的人数为4人,
所以分数在[90,100)范围内的学生数为8-4=4.
从表中可知分数在[70,90)范围内的频率为0.25,所以有20×0.25=5(人),所以20人中数学成绩及格的学生为13人.
所以估计全校数学成绩及格率为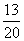 =65%.
=65%.
(2)设A表示事件“从大于等于110分的学生中随机选2名学生得分,平均得分大于等于130分”,由茎叶图可知大于等于110分有5人,记这5人分别为m,n,c,d,e,则选取学生的所有可能结果为:
(m,n),(m,c),(m,d),(m,e),(n,c),(n,d),(n,e),(c,d),(c,e),(d,e),基本事件数为10,事件“2名学生的平均得分大于等于130分”也就是“这2名学生的分数之和大于等于260分”,所以可能结果为:(118,142),(128,136),(128,142),(136,142),共4种情况,基本事件数为4,所以P(A)=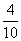 =
=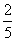 .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
三棱锥A BCD及其侧视图、俯视图如图14所示.设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP.
(1)证明:P是线段BC的中点;
(2)求二面角A NP M的余弦值.
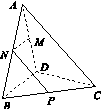
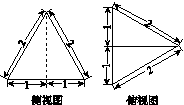
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
如图X261所示,在正方体ABCD A1B1C1D1中,M,N分别是棱C1D1,C1C的中点.给出以下四个结论:
①直线AM与直线C1C相交;
②直线AM与直线BN平行;
③直线AM与直线DD1异面;
④直线BN与直线MB1异面.
其中正确结论的序号为________(填入所有正确结论的序号).
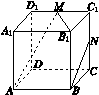
图X261
查看答案和解析>>
科目:高中数学 来源: 题型:
由于当前学生课业负担较重,造成青少年视力普遍下降,现从某中学随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:

(1)若视力测试结果不低于5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(2)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记ξ表示抽到“好视力”学生的人数,求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
一盒中有12个乒乓球,其中9个新的,3个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球个数X是一个随机变量,其分布列为P(X),则P(X=4)的值为( )
A.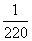 B.
B.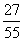
C.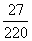 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
设随机变量X的概率分布列如下表所示:
| X | 0 | 1 | 2 |
| P | a |
|
|
F(x)=P(X≤x),则当x的取值范围是[1,2)时,F(x)等于( )
A.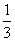 B.
B.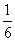
C.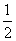 D.
D.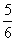
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com