
分析 (1)分别求出f(x),g(x)的导数,计算得到f′(1)=g′(1),求出a的值即可;
(2)问题转化为1-a≥$\frac{{x}^{2}+x+1}{{e}^{x}}$在[01,]恒成立,令h(x)=$\frac{{x}^{2}+x+1}{{e}^{x}}$,x∈[0,1],根据函数的单调性求出h(x)的最大值,得到关于a的不等式,解出即可.
解答 解:(1)f′(x)=$\frac{-x}{{e}^{x}}$,f′(1)=-$\frac{1}{e}$,
g′(x)=-2ax,g′(1)=-2a,
由题意得:-2a=-$\frac{1}{e}$,解得:a=$\frac{1}{2e}$;
(2)当x∈[0,1]时,不等式f(x)≤g(x)恒成立,
即1-a≥$\frac{{x}^{2}+x+1}{{e}^{x}}$在[0,1]恒成立,
令h(x)=$\frac{{x}^{2}+x+1}{{e}^{x}}$,x∈[0,1],
则h′(x)=$\frac{-x(x-1)}{{e}^{x}}$≥0,
故h(x)在[0,1]递增,
故h(x)≤h(1)=$\frac{3}{e}$,
故1-a≥$\frac{3}{e}$,解得:a≤$\frac{e-3}{3}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | -2 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,PA=PD,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l.
如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,PA=PD,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{π}{2}$) | B. | (-$\frac{π}{4}$,$\frac{π}{4}$) | C. | (-$\frac{π}{2}$,-$\frac{π}{4}$) | D. | ($\frac{π}{4}$,$\frac{3π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
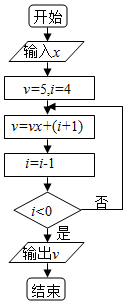 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法至今仍是比较先进的算法.如图的程序框图是针对某一多项式求值的算法,如果输入的x的值为2,则输出的v的值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法至今仍是比较先进的算法.如图的程序框图是针对某一多项式求值的算法,如果输入的x的值为2,则输出的v的值为( )| A. | 129 | B. | 144 | C. | 258 | D. | 289 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com