
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{16}$ |
分析 设把长为80cm的铁丝随机截成三段的长度分别为x,y,80-x-y,则由题意知$\left\{\begin{array}{l}{80≥x≥20}\\{80≥y≥20}\\{80≥80-x-y≥20}\end{array}\right.$,以面积为测度,即可求出概率.
解答 解:设把长为80cm的铁丝随机截成三段的长度分别为x,y,80-x-y,
则由题意知$\left\{\begin{array}{l}{80≥x≥20}\\{80≥y≥20}\\{80≥80-x-y≥20}\end{array}\right.$,
所以包含事件每段铁丝长度都不小于20cm所表示的面积为区域的面积为$\frac{1}{2}×20×20$=200,
而基本事件所表示的平面$\frac{1}{2}×$80×80=3200,
所以由几何概型的计算公式即可得出每段铁丝长度都不小于20cm的概率为$\frac{1}{16}$.
故选A.
点评 本题考查几何概型,考查面积的计算,属于中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{\sqrt{3}}{2}$,1) | B. | [$\frac{\sqrt{6}}{3}$,1) | C. | (0,$\frac{\sqrt{3}}{2}$] | D. | (0,$\frac{\sqrt{6}}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
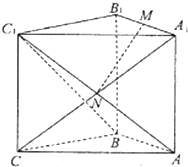 直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1,M为A1B1的中点,N是AC1与A1C的交点.
直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1,M为A1B1的中点,N是AC1与A1C的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
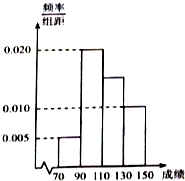 某班一次数学考试成绩频率分布直方图如图所示,数据分组依次为[70,90),[90,110),[110,130),[130,150],已知成绩大于等于90分的人数为36人,现采用分层抽样的方式抽取一个容量为10的样本.
某班一次数学考试成绩频率分布直方图如图所示,数据分组依次为[70,90),[90,110),[110,130),[130,150],已知成绩大于等于90分的人数为36人,现采用分层抽样的方式抽取一个容量为10的样本.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com