
(本题满分14分)
某零售店近五个月的销售额和利润额资料如下表:
| 商店名称 | A | B | C | D | E |
销售额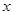 (千万元) (千万元) | 3 | 5 | 6 | 7 | 9 9 |
利润额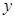 (百万元) (百万元) | 2 | 3 | 3 | 4 | 5 |
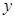 关于销售额
关于销售额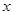 的回归直线方程;
的回归直线方程; 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
在对人们的休闲方式的一次调查中,共调查了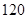 人,其中女性
人,其中女性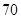 人,男性
人,男性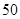 人.女性中有
人.女性中有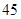 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外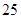 人主要的休闲方式是运动;男性中有
人主要的休闲方式是运动;男性中有 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外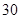 人主要的休闲方式是运动.
人主要的休闲方式是运动.
(1)根据以上数据建立一个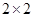 的列联表;
的列联表;
(2)判断性别与休闲方式是否有关系.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成6组后,得到部分频率分布直方图(如图),观察图中的信息,回答下列问题.
(Ⅰ)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(Ⅱ)根据频率分布直方图,估计本次考试的平均分;
(Ⅲ)若从60名学生中随机抽取2人,抽到的学生成绩在[40,70)记0分,记[70,100]记1分,用X表示抽取结束后的总记分,求X的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
 (1)根据上表完成下面的2×2列联表(单位:人):
(1)根据上表完成下面的2×2列联表(单位:人):| | 数学成绩优秀 | 数学成绩不优秀 | 合 计 |
| 物理成绩优秀 | | | |
| 物理成绩不优秀 | | | |
| 合 计 | | | 20 |
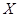 和
和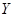 ,它们的值域分别为
,它们的值域分别为 和
和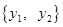 ,其样本频数列联表(称为
,其样本频数列联表(称为 列联表)为:
列联表)为:| | 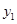 | 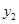 | 合计 |
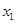 | 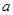 |  | 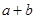 |
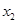 |  | 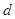 | 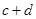 |
| 合计 | 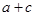 | 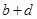 |  |
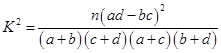 ,其中
,其中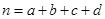 为样本容量;
为样本容量;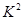 的临界值参考表:
的临界值参考表: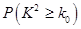 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分)我校高二(1)班男同学有45名,女同学有15名,按照分层抽样的方法组建了一个4人的课外兴趣小组.
(1)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(2)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出1名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
(3)试验结束后,第一次做试验的同学得到的试验数据为68,70,71,72,74,第二次做试验的同学得到的试验数据为69,70,70,72,74,请问哪位同学的实验更稳定?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2013年春节前,有超过20万名广西、四川等省籍的外来务工人员选择驾乘摩托车沿321国道长途跋涉返乡过年,为防止摩托车驾驶人因长途疲劳驾驶,手脚僵硬影响驾驶操作而引发交事故,肇庆市公安交警部门在321国道沿线设立了多个长途行驶摩托车驾乘人员休息站,让过往返乡过年的摩托车驾驶人有一个停车休息的场所。交警小李在某休息站连续5天对进站休息的驾驶人员每隔50辆摩托车就进行省籍询问一次,询问结果如图所示:
(1)问交警小李对进站休息的驾驶人员的省籍询问采用的是什么抽样方法?
(2)用分层抽样的方法对被询问了省籍的驾驶人员进行抽样,若广西籍的有5名,则四川籍的应抽取几名?
(3)在上述抽出的驾驶人员中任取2名,求抽取的2名驾驶人员中四川籍人数 的分布列及其数学期望。
的分布列及其数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
PM2. 5是指大气中直径小于或等于2. 5微米的颗粒物,也称为 可人肺颗粒物.我国PM2. 5标准采用世卫组织设定的最宽限 值,即PM2.5日均值在35微克/立方米以下空气质量为一级; 在35微克/立方米~75微克/立方米之间空气质量为二级;在 75微克/立方米以上空气质量为超标.
某市环保局从市区2012年全年每天的PM2.5监测数据中 随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为 茎,个位为叶)
(I)从这9天的数据中任取2天的数据,求恰有一天空气质量达到一级的概率;
(II) 以这9天的PM2. 5日均值来估计供暖期间的空气质量情况,则供暖期间(按150天计算)中大约有多少天的空气质量达到一级.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
通过市场调查,得到某产品的资金投入x(万元)与获得的利润y(万元)的数据,如表所示:
| 资金投入x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 6 | 9 |
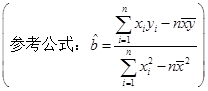
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量( 吨)与相应的生产能耗
吨)与相应的生产能耗 (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
 | 3 | 4 | 5 | 6 |
 | 2.5 | 3 | 4 | 4.5 |
 关于
关于 的线性回归方程
的线性回归方程 ;
; ,
, )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com