
如图所示的两个同心圆盘均被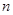 等分(
等分(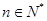 且
且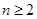 ),在相重叠的扇形格中依次同时填上
),在相重叠的扇形格中依次同时填上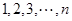 ,内圆盘可绕圆心旋转,每次可旋转一个扇形格,当内圆盘旋转到某一位置时,定义所有重叠扇形格中两数之积的和为此位置的“旋转和”.
,内圆盘可绕圆心旋转,每次可旋转一个扇形格,当内圆盘旋转到某一位置时,定义所有重叠扇形格中两数之积的和为此位置的“旋转和”.
(1)求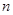 个不同位置的“旋转和”的和;
个不同位置的“旋转和”的和;
(2)当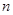 为偶数时,求
为偶数时,求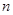 个不同位置的“旋转和”的最小值;
个不同位置的“旋转和”的最小值;
(3)设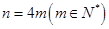 ,在如图所示的初始位置将任意
,在如图所示的初始位置将任意 对重叠的扇形格中的两数均改写为0,证明:当
对重叠的扇形格中的两数均改写为0,证明:当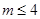 时,通过旋转,总存在一个位置,任意重叠的扇形格中两数不同时为0.
时,通过旋转,总存在一个位置,任意重叠的扇形格中两数不同时为0.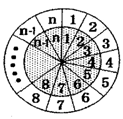
(1)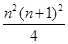 ;(2) 最小值
;(2) 最小值 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)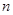 个不同位置的“旋转和”的和,就是将所有位置的旋转相加,故内盘中的任一数都会和外盘中的每个数作积;(2)设内盘中的
个不同位置的“旋转和”的和,就是将所有位置的旋转相加,故内盘中的任一数都会和外盘中的每个数作积;(2)设内盘中的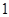 和外盘中的
和外盘中的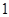 同扇形格时的“旋转和”为
同扇形格时的“旋转和”为 ;设内盘中的
;设内盘中的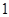 和外盘中的
和外盘中的 同扇形格时的“旋转和”为
同扇形格时的“旋转和”为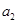 ;依次下去,设内盘中的
;依次下去,设内盘中的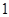 和外盘中的
和外盘中的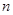 同扇形格时的“旋转和”为
同扇形格时的“旋转和”为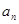 ;这样便得一个数列.这样问题转化为求该数列的最小值.求数列的最值,首先研究数列的单调性,而研究数列的单调性,就是研究相邻两项的差的符号,即研究
;这样便得一个数列.这样问题转化为求该数列的最小值.求数列的最值,首先研究数列的单调性,而研究数列的单调性,就是研究相邻两项的差的符号,即研究 的符号;(3)显然直接证明有点困难,故采用反证法.由于该问题只涉及0与非0的问题,故可将图中所有非
的符号;(3)显然直接证明有点困难,故采用反证法.由于该问题只涉及0与非0的问题,故可将图中所有非 数改写为
数改写为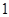 ,这样共有
,这样共有 个0,
个0, 个1.假设任意位置,总存在一个重叠的扇形格中两数同时为
个1.假设任意位置,总存在一个重叠的扇形格中两数同时为 ,则此位置的“旋转和”必大于或等于
,则此位置的“旋转和”必大于或等于 ,初始位置外的
,初始位置外的 个位置的“旋转和”的和为
个位置的“旋转和”的和为 ,则有
,则有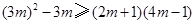 ,即
,即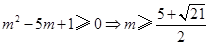 ,这与
,这与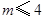 矛盾,故命题得证.
矛盾,故命题得证.
试题解析:(1)由于内盘中的任一数都会和外盘中的每个作积,故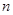 个不同位置的“旋转和”的和为
个不同位置的“旋转和”的和为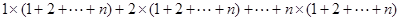
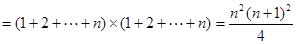 ; 3分
; 3分
(2)设内盘中的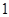 和外盘中的
和外盘中的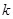 同扇形格时的“旋转和”为
同扇形格时的“旋转和”为
则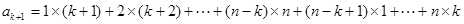
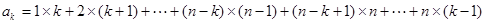

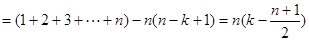 5分
5分
所以当 时,
时,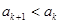 ,当
,当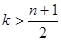 时,
时, ,所以
,所以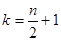 时,
时, 最小
最小
最小值

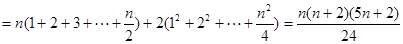 ; 8分
; 8分
(3)证明:将图中所有非 数改写为
数改写为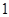 ,现假设任意位置,总存在一个重叠的扇形格中两数同时为
,现假设任意位置,总存在一个重叠的扇形格中两数同时为 ,则此位置的“旋转和”必大于或等于
,则此位置的“旋转和”必大于或等于 ,初始位置外的
,初始位置外的 个位置的“旋转和”的和为
个位置的“旋转和”的和为 ,则有
,则有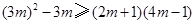 ,即
,即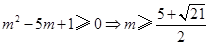 ,这与
,这与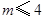 矛盾,故命题得证. 12分
矛盾,故命题得证. 12分
考点:数列及数列的和.


科目:高中数学 来源: 题型:解答题
如果数列 满足:
满足: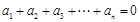 且
且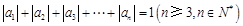 ,则称数列
,则称数列 为
为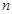 阶“归化数列”.
阶“归化数列”.
(1)若某4阶“归化数列” 是等比数列,写出该数列的各项;
是等比数列,写出该数列的各项;
(2)若某11阶“归化数列” 是等差数列,求该数列的通项公式;
是等差数列,求该数列的通项公式;
(3)若 为n阶“归化数列”,求证:
为n阶“归化数列”,求证: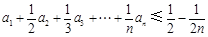 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列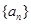 的前
的前 项和
项和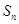 和通项
和通项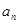 满足
满足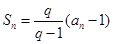 (
(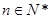 ,
,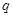 是大于0的常数,且
是大于0的常数,且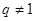 ),数列
),数列 是公比不为
是公比不为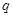 的等比数列,
的等比数列,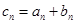 .
.
(1)求数列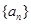 的通项公式;
的通项公式;
(2)设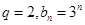 ,是否存在实数
,是否存在实数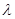 ,使数列
,使数列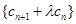 是等比数列?若存在,求出所有可能的实数
是等比数列?若存在,求出所有可能的实数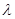 的值,若不存在说明理由;
的值,若不存在说明理由;
(3)数列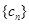 是否能为等比数列?若能,请给出一个符合的条件的
是否能为等比数列?若能,请给出一个符合的条件的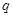 和
和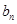 的组合,若不能,请说明理由.
的组合,若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设项数均为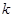 (
(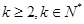 )的数列
)的数列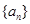 、
、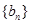 、
、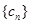 前
前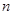 项的和分别为
项的和分别为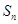 、
、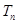 、
、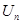 .已知集合
.已知集合 =
=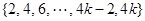 .
.
(1)已知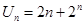 ,求数列
,求数列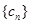 的通项公式;
的通项公式;
(2)若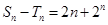
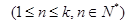 ,试研究
,试研究 和
和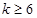 时是否存在符合条件的数列对(
时是否存在符合条件的数列对(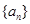 ,
,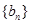 ),并说明理由;
),并说明理由;
(3)若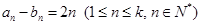 ,对于固定的
,对于固定的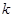 ,求证:符合条件的数列对(
,求证:符合条件的数列对(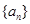 ,
,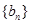 )有偶数对.
)有偶数对.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com