在平面直角坐标系xOy中，直线l：x＋y＋2＝0在矩阵M＝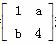
对应的变换作用下得到直线m：x－y－4＝0，求实数a、b的值．
解：(解法1)在直线l：x＋y＋2＝0上取两点A(－2，0)，B(0，－2)，A、B在矩阵M对应的变换作用下分别对应于点A′、B′，因为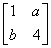
＝
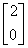
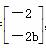，所以A′的坐标为(－2，－2b)；
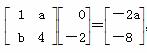，所以B′的坐标为(－2a，－8)．由题意A′、B′在直线m：x－y－4＝0上，所以
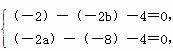解得a＝2，b＝3.
(解法2)设直线l：x＋y＋2＝0上任意一点(x，y)在矩阵M对应的变换作用下对应于点(x′，y′)．因为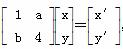
，所以x′＝x＋ay，y′＝bx＋4y.因为(x′，y′)在直线m上，所以(x＋ay)－(bx＋4y)－4＝0，即(1－b)x＋(a－4)y－4＝0.
又点(x，y)在直线x＋y＋2＝0上，
所以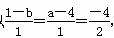
，解得a＝2，b＝3.
科目：高中数学 来源： 题型：
已知△ABC的内角为A、B、C，其对边分别为a、b、c，B为锐角，向量m＝(2sin B，－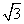
)，n＝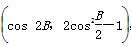
，且m∥n.
(1)求角B的大小；
(2)如果b＝2，求S△ABC的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知函数f(x)＝|2x－1|＋|2x＋a|，g(x)＝x＋3.
(1)当a＝－2时，求不等式f(x)<g(x)的解集；
(2)设a>－1时，且当x∈
时，f(x)≤g(x)，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知直线l：ax＋y＝1在矩阵A＝
对应的变换作用下变为直线l′：x＋by＝1.
(1) 求实数a、b的值；
(2) 若点P(x0，y0)在直线l上，且A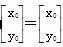
，求点P的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
设矩阵M＝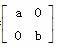
(其中a>0，b>0)．
(1) 若a＝2，b＝3，求矩阵M的逆矩阵M－1；
(2) 若曲线C：x2＋y2＝1在矩阵M所对应的线性变换作用下得到曲线C′：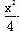
＋y2＝1，求a、b的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，求x＋y＋z的值．
对应的变换作用下得到的图形．
，若矩阵M的逆矩阵M －1＝
，求a、b的值．
，求AF的长．