
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且![]() .D为线段AC的中点.
.D为线段AC的中点.
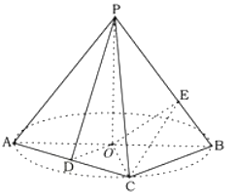
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若点E在线段PB上,且![]() ,求三棱锥
,求三棱锥![]() 体积的最大值.
体积的最大值.
【答案】(1)证明见解析;(2)24.
【解析】
(1)由已知先证明AC⊥OD,又PO⊥AC,从而得到AC⊥平面PDO,进而证明平面PAC⊥平面PDO;
(2)由题意先求得△ABC面积的最大值,进而求得三棱锥PABC体积的最大值,从而求得三棱锥EPOC体积的最大值.
(1)证明:在ΔAOC中,因为OA=OC,D为AC的中点,所以AC⊥OD,
又PO垂直于圆O所在的平面,所以PO⊥AC;
又DO∩PO=O,所以AC⊥平面PDO;
又AC![]() 平面PAC,
平面PAC,
所以平面PAC⊥平面PDO;
(2)由PE=![]() PB,则
PB,则![]()
所以V三梭锥E-POC=V三棱锥C-POE=![]() V三棱维C-POB=
V三棱维C-POB=![]() S三棱维P-OCB=
S三棱维P-OCB=![]() V三棱维P-ACB
V三棱维P-ACB
又点C在圆O.上,所以当CO⊥AB时,C到AB的距离最大,且最大值为6;
又AB=12,所以ΔABC面积的最大值为![]() ×12×6=36;
×12×6=36;
又三棱锥P-ABC的高为PO=6,
所以三棱锥P-ABC体积的最大值为![]() ×36×6=72;
×36×6=72;

综上知,三棱锥E-POC体积的最大值为![]() ×72=24.
×72=24.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列命题正确的有________(填序号)
①已知![]() 或
或![]() ,
,![]() ,则p是q的充分不必要条件;
,则p是q的充分不必要条件;
②“函数![]() 的最小正周期为
的最小正周期为![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
③![]() 中,内角A,B,C所对的边分别为a,b,c,
中,内角A,B,C所对的边分别为a,b,c,![]() ,
,![]() ,则“
,则“![]() ”是“
”是“![]() 为等腰三角形”的必要不充分条件;
为等腰三角形”的必要不充分条件;
④若命题![]() “函数
“函数![]() 的值域为
的值域为![]() ”为真命题,则实数a的取值范围是
”为真命题,则实数a的取值范围是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:关于x的方程x![]() a在(1,+∞)上有实根;命题q:方程
a在(1,+∞)上有实根;命题q:方程![]() 1表示的曲线是焦点在x轴上的椭圆.
1表示的曲线是焦点在x轴上的椭圆.
(1)若p是真命题,求a的取值范围;
(2)若p∧q是真命题,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
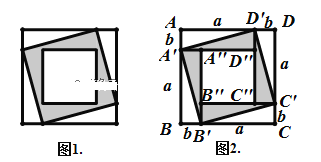
【题目】下图1,是某设计员为一种商品设计的平面logo样式.主体是由内而外的三个正方形构成.该图的设计构思如图2,中间正方形![]() 的四个顶点,分别在最外围正方形ABCD的边上,且分所在边为a,b两段.设中间阴影部分的面积为
的四个顶点,分别在最外围正方形ABCD的边上,且分所在边为a,b两段.设中间阴影部分的面积为![]() ,最内正方形
,最内正方形![]() 的面积为
的面积为![]() .当
.当![]() ,且
,且![]() 取最大值时,定型该logo的最终样式,则此时a,b的取值分别为_____________.
取最大值时,定型该logo的最终样式,则此时a,b的取值分别为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
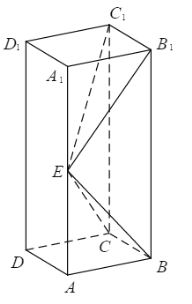
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B–EC–C1的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com