Question

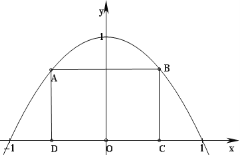
【题目】如图所示，抛物线与轴所围成的区域是一块等待开垦的土地，现计划在该区域内围出一块矩形地块ABCD作为工业用地，其中A、B在抛物线上，C、D在轴上.已知工业用地每单位面积价值为元，其它的三个边角地块每单位面积价值元.

（1）求等待开垦土地的面积；

（2）如何确定点C的位置，才能使得整块土地总价值最大.

Answer 1

【答案】（1）;（2）点C的坐标为.

【解析】

试题分析：（1）由于等待开垦土地是由曲线与x轴围成的，求出曲线与x轴的交点坐标，再用定积分就可求出此块土地的面积；（2）既然要确定点C的位置，使得整块土地总价值最大,那我们只需先设出点C的坐标为(x，0)，然后含x的代数式表示出矩形地块ABCD，进而结合（1）的结果就可表示出其它的三个边角地块的面积，从而就能将整块土地总价值表示成为x的函数，再利用导数求此函数的最大值即可．

试题解析：（1）由于曲线与x轴的交点坐标为（－１，0）和(１,0),所以所求面积S=，

故等待开垦土地的面积为 3分

（2）设点C的坐标为，则点B其中，

∴ 5分

∴土地总价值 7分

由得 9分

并且当时，

故当时，y取得最大值. 12分

答：当点C的坐标为时，整个地块的总价值最大. 13分