考点:利用导数研究函数的单调性,导数在最大值、最小值问题中的应用
专题:函数的性质及应用,导数的综合应用
分析:对第(1)问,先求导,再通过一元二次方程的实根讨论单调性;
对第(2)问,可将f(x
0)=f(
)转化为f(x
0)-f(
)=0,即将“函数问题”化为“方程是否有实根问题”处理.
解答:
解:(1)由f(x)得f′(x)=x
2+2x+a,
令f′(x)=0,即x
2+2x+a=0,判别式△=4-4a,
①当△≤0即a≥1时,f′(x)≥0,则f(x)在(-∞,+∞)上为增函数.
②当△>0即a<1时,方程f′(x)=0的两根为
,即
-1±,
当x∈(-∞,-1-
)时,f′(x)>0,则f(x)为增函数;
当
x∈(-1-,-1+)时,f′(x)<0,则f(x)为减函数;
当
x∈(-1+,+∞)时,f′(x)>0,则f(x)为增函数.
综合①、②知,a≥1时,f(x)的单调递增区间为(-∞,+∞),
a<1时,f(x)的单调递增区间为(-∞,
-1-)和
(-1+,+∞),
f(x)的单调递减区间为
(-1-,-1+).
(2)∵
f(x)-f()=
x3+x2+ax+1-[×()3+()2+a×+1]=
[x3-()3]+[x2-()2]+a(x-)=
[(x-)(x2++)]+(x+)(x-)+a(x-)=
(x-)(+++a)=
(x-)(4x2+14x+7+12a).
∴若存在
x0∈(0,)∪
(,1),使得
f(x0)=f(),即
f(x0)-f()=0,
则关于x的方程4x
2+14x+7+12a=0在
(0,)∪
(,1)内必有实数解.
∵a<0,∴△=14
2-16(7+12a)=4(21-48a)>0,
方程4x
2+14x+7+12a=0的两根为
,即
,
∵x
0>0,∴
x0=,
依题意有
0<<1,且
≠,
即
7<<11,且
≠9,∴49<21-48a<121,且21-48a≠81,
得
-<a<-,且
a≠-.
∴当
a∈(-,-)∪
(-,-)时,存在唯一的
x0∈(0,)∪
(,1),使得
f(x0)=f()成立;
当
a∈(-∞,-]∪
[-,0)∪{
-}时,不存在
x0∈(0,)∪
(,1),使得
f(x0)=f()成立.
点评:1.求含参数的函数的单调区间时,导函数的符号往往难以确定,如果受到参数的影响,应对参数进行讨论,讨论的标准要根据导函数解析式的特征而定.如本题中导函数为一元二次函数,就有必要考虑对应方程中的判别式△.
2.对于存在性问题,一般先假设所判断的问题成立,再由假设去推导,若求得符合题意的结果,则存在;若得出矛盾,则不存在.



 如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.
如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.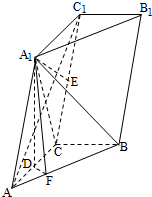 如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.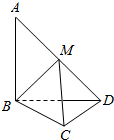 在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.
在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.