
某房地产公司要在荒地ABCDE(如图所示)上划出一块长方形地面建造一幢公寓,问:如何设计才能使公寓占地面积最大?求出最大面积(尺寸单位:m).
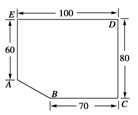
.
[解析] 如图所示,设计长方形公寓分三种情况:
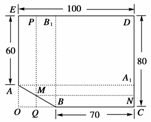
(1)当一顶点在BC上时,只有在B点时长方形BCDB1面积最大,
∴S1=SBCDB1=5600m2.
(2)当一顶点在EA边上时,只有在A点时长方形AA1DE的面积最大,
∴S2=SAA1DE=6 000m2.
(3)当一顶点在AB边上时,设该点为M,则可构造长方形MNDP,并补出长方形OCDE.
设MQ=x(0≤x≤20),∴MP=PQ-MQ=80-x.
又OA=20,OB=30,则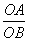 =
=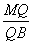 ,
,
∴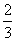 =
=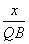 ,∴QB=
,∴QB=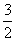 x,
x,
∴MN=QC=QB+BC=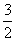 x+70,
x+70,
∴S3=SMNDP=MN·MP=(70+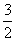 x)·(80-x)
x)·(80-x)
=-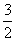 (x-
(x-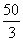 )2+
)2+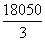 ,
,
当x=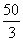 时,S3=
时,S3=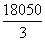 .比较S1,S2,S3,得S3最大,
.比较S1,S2,S3,得S3最大,
此时MQ=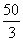 m,BM=
m,BM=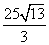 m,
m,
故当长方形一顶点落在AB边上离B点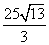 m处时公寓占地面积最大,最大面积为
m处时公寓占地面积最大,最大面积为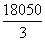 m2.
m2.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:高中数学 来源: 题型:
已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2-2x.
(1)画出偶函数f(x)的图像;
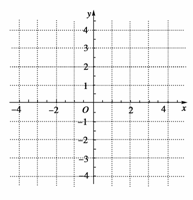
(2)根据图像,写出f(x)的单调区间;同时写出函数的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
关于函数y=2x2-2x-3有以下4个结论:
①定义域为(-∞,-1)∪(3,+∞);
②递增区间为[1,+∞);
③是非奇非偶函数;
④值域是(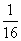 ,+∞).
,+∞).
则正确的结论是________.(填序号即可)
查看答案和解析>>
科目:高中数学 来源: 题型:
某商品零售价2014年比2013年上涨25%,欲控制2015年比2013年只上涨10%,则2015年应比2014年降价( )
A.15% B.12%
C.10% D.50%
查看答案和解析>>
科目:高中数学 来源: 题型:
江岸边有一炮台高30m,江中有两条船,由炮台顶部测得俯角分别为45°和60°,而且两条船与炮台底部连线成30°角,则两条船相距( )
A.10 m B.100
m B.100 m
m
C.20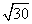 m D.30m
m D.30m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com