练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    江岸边有一炮台高30m，江中有两条船，由炮台顶部测得俯角分别为45°和60°，而且两条船与炮台底部连线成30°角，则两条船相距(　　)

    A．10m                                                   B．100m

    C．20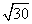m                                                 D．30m


    A

    [解析]　设炮塔顶A、底D，两船B、C，则∠BAD＝45°，∠CAD＝30°，∠BDC＝30°，AD＝30，∴DB＝30，DC＝10，BC2＝DB2＋DC2－2DB·DC·cos30°＝300，

    ∴BC＝10.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某房地产公司要在荒地ABCDE(如图所示)上划出一块长方形地面建造一幢公寓，问：如何设计才能使公寓占地面积最大？求出最大面积(尺寸单位：m)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，三个内角A、B、C的对边分别为a、b、c.若b＝，B＝，tanC＝2，则c＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a、b、c分别为△ABC三个内角A、B、C的对边，c＝asinC－ccosA.

    (1)求A；

    (2)若a＝2，△ABC的面积为，求b、c.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，海岸线上有相距5n mile的两座灯塔A、B，灯塔B位于灯塔A的正南方向．海上停泊着两艘轮船，甲船位于灯塔A的北偏西75°方向，与A相距3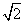n mile的D处；乙船位于灯塔B的北偏西60°方向，与B相距5n mile的C处，则两艘轮船之间的距离为(　　)

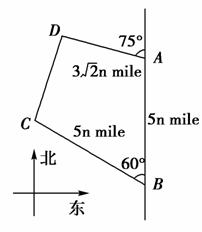
    A．5n mile                                                     B．2n mile

    C.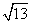n mile                                                 D．3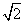n mile

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在海岛A上有一座海拔1 km的山峰，山顶设有一个观察站P，有一艘轮船按一固定方向做匀速直线航行，上午11：00时，测得此船在岛北偏东15°、俯角为30°的B处，到11：10时，又测得该船在岛北偏西45°、俯角为60°的C处．

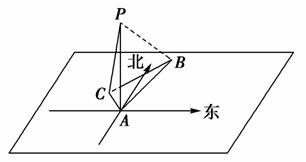
    (1)求船的航行速度；

    (2)求船从B到C行驶过程中与观察站P的最短距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a、b都是非零向量，下列四个条件中，使＝成立的充分条件是(　　)

    A．a＝－b                                                    B．a∥b

    C．a＝2b                                                      D．a∥b且|a|＝|b|

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC所在的平面内有一点P，满足，则△PBC与△ABC的面积之比是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知△ABC中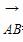，＝a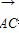，＝b，a·b<0，S△ABC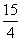＝，|a|＝3，|b|＝5，则∠BAC等于(　　)

    A．30°                                                          B．120°

    C．150°                                                        D．30°或150°

    查看答案和解析>>

    同步练习册答案