
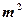 的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度
的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度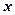 不得
不得 超过
超过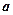 米,房屋正面的造价为400元
米,房屋正面的造价为400元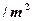 ,房屋侧面的造价为150元
,房屋侧面的造价为150元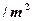 ,屋顶和底面的造价费用合计为5800元,如果墙高为3米.且不计房屋背面的费用.
,屋顶和底面的造价费用合计为5800元,如果墙高为3米.且不计房屋背面的费用. 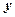 表示成
表示成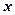 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域; 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
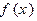 是定义在
是定义在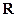 上的函数,对任意实数
上的函数,对任意实数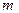 、
、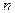 ,都有
,都有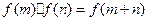 ,且当
,且当 <0时,
<0时,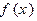 >1.
>1.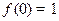 ;
; >0时,0<
>0时,0<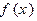 <1;
<1;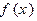 是
是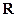 上的减函数;
上的减函数;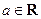 ,试解关于
,试解关于 的不等式
的不等式 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 池向居民小区不间断地供水,且
池向居民小区不间断地供水,且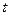 小时内供水总量为
小时内供水总量为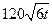 吨(
吨(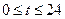 )。⑴供水开始几小时后,蓄水池中的水量最小?最小水量为多少吨?⑵若蓄水池中的水量少于80吨,就会出现供水紧张现象,试问在一天的24小时内,有多少小时会出现供水紧张现象?并说明理由。
)。⑴供水开始几小时后,蓄水池中的水量最小?最小水量为多少吨?⑵若蓄水池中的水量少于80吨,就会出现供水紧张现象,试问在一天的24小时内,有多少小时会出现供水紧张现象?并说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
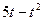 (百万元)。
(百万元)。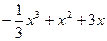 (百万元),请设计资金分配方案,使该公司由
(百万元),请设计资金分配方案,使该公司由 此获得的收益最大。(注:收益=销售额—投入)
此获得的收益最大。(注:收益=销售额—投入)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com