Question

18．直线y=x+a与抛物线y²=5ax（a＞0）相交于A，B两点，C（0，2a），给出下列4个命题：
p₁：△ABC的重心在定直线7x-3y=0上，p₂：|AB|$\sqrt{3-a}$的最大值为2$\sqrt{10}$；
p₃：△ABC的重心在定直线 3x-7y=0上；p₄：|AB|$\sqrt{3-a}$的最大值为2$\sqrt{5}$．
其中的真命题为（　　）

• A． p₁，p₂
• B． p₁，p₄
• C． p₂，p₃
• D． p₃，p₄

Answer 1

分析 联立直线方程与抛物线方程，化为关于x的一元二次方程，利用根与系数的关系及重心坐标公式求出△ABC的重心坐标，可知p₁为真命题，再由弦长公式求得|AB|，代入|AB|$\sqrt{3-a}$利用导数求其最大值可知命题p₂是真命题，p₄是假命题，则答案可求．

解答 解：如图，
联立$\left\{\begin{array}{l}{y=x+a}\\{{y}^{2}=5ax}\end{array}\right.$，得x²-3ax+a²=0．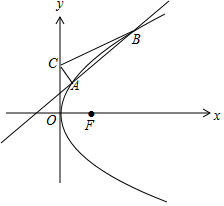
△=9a²-4a²=5a²＞0．
设A（x₁，y₁），B（x₂，y₂），
则x₁+x₂=3a，${x}_{1}{x}_{2}={a}^{2}$．
∴y₁+y₂=x₁+x₂+2a=5a，
∵C（0，2a），由重心坐标公式可得：△ABC的重心坐标为（$\frac{3a+0}{3}$，$\frac{5a+2a}{3}$）=（a，$\frac{7a}{3}$）．
把点（a，$\frac{7a}{3}$）代入7x-3y=0成立，代入 3x-7y=0不成立，
∴命题p₁是真命题，p₃是假命题；
|AB|=$\sqrt{2}|{x}_{1}-{x}_{2}|=\sqrt{2}\sqrt{（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}•\sqrt{9{a}^{2}-4{a}^{2}}=\sqrt{10}|a|=\sqrt{10}a$．
∴|AB|$\sqrt{3-a}$=$\sqrt{10}•\sqrt{3{a}^{2}-{a}^{3}}$，
令g（a）=-a³+3a²（a＞0），则g′（a）=-3a²+6a=-3a（a-2），
当a∈（0，2）时，g′（a）＞0，当a∈（2，+∞）时，g′（a）＜0，
∴g（a）在（0，2）上为增函数，在（2，+∞）上为减函数，
则g（a）_max=g（2）=4，
∴|AB|$\sqrt{3-a}$的最大值为$2\sqrt{10}$，
∴命题p₂是真命题，p₄是假命题．
∴真命题是p₁，p₂ ．
故选：A．

点评 本题考查抛物线的简单性质，考查直线与抛物线位置关系的应用，训练了利用导数求最值，是中档题．