
【题目】某同学在研究性学习中,关于三角形与三角函数知识的应用(约定三内角![]() 所对的边分别是
所对的边分别是![]() )得出如下一些结论:
)得出如下一些结论:
(1)若![]() 是钝角三角形,则
是钝角三角形,则![]() ;
;
(2)若![]() 是锐角三角形,则
是锐角三角形,则![]() ;
;
(3)在三角形![]() 中,若
中,若![]() ,则
,则![]()
(4)在![]() 中,若
中,若![]() ,则
,则![]()
其中错误命题的个数是 ( )
A. 0 B. 1 C. 2 D. 3
【答案】D
【解析】(1)∵tanA+tanB=tan(A+B)(1tanAtanB),
∴tanA+tanB+tanC=tan(A+B)(1tanAtanB)+tanC=tanAtanBtanC,
∴△ABC是钝角三角形,可得:tanAtanBtanC<0,故错误;
(2)∵△ABC为锐角三角形,
∴A+B>90°, B>90°A,
∴cosB<sinA,sinB>cosA,
∴cosBsinA<0,sinBcosA>0,
∴cosBsinA<sinBcosA,可得cosA+cosB<sinA+sinB,故错误;
(3)当![]() 时,tanB不存在,故错误;
时,tanB不存在,故错误;
(4)由![]() 得到0<C<90°,且
得到0<C<90°,且![]() ,
,
因为正切函数在(0,90°)为增函数,所以得到30°<C<45°;
由![]() 可得到0<B<90°或90°<B<180°,
可得到0<B<90°或90°<B<180°,
在0<B<90°时, ![]() ,因为正弦函数在(0,90°)为增函数,得到0<B<30°;
,因为正弦函数在(0,90°)为增函数,得到0<B<30°;
在90°<B<180°时, ![]() ,但是正弦函数在90°<B<180°为减函数,得到B>150°,则B+C>180°,
,但是正弦函数在90°<B<180°为减函数,得到B>150°,则B+C>180°,
矛盾,不成立。
所以0<B<30°.由B和C的取值得到A为钝角,
所以A>C>B,故正确;
本题选择D选项.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足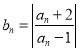 ,其中
,其中![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表达式(不必写出证明过程);
的表达式(不必写出证明过程);
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() .
.
(B)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表达式(不必写出证明过程);
的表达式(不必写出证明过程);
(2)设![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(4,-3),B(2,-1)和直线l:4x+3y-2=0.
(1)求在直角坐标平面内满足|PA|=|PB|的点P的方程;
(2)求在直角坐标平面内一点P满足|PA|=|PB|且点P到直线l的距离为2的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是 ( )
A. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内一定存在直线平行于平面
内一定存在直线平行于平面![]()
B. 如果平面![]() 不垂直平面
不垂直平面![]() ,那么平面
,那么平面![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面![]()
C. 如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,那么
,那么![]()
D. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内所有直线都垂直于平面
内所有直线都垂直于平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .求实数
.求实数![]() 的值;
的值;
(2)①若![]() 时,函数
时,函数![]() 既有极大值,又有极小值,求实数
既有极大值,又有极小值,求实数![]() 的取值范围;
的取值范围;
②若![]() ,若
,若![]() 对一切正实数
对一切正实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围(用
的取值范围(用![]() 表示).
表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,![]() 是公比为
是公比为![]() 的等比数列. 记
的等比数列. 记![]() .
.
(1)求证: 数列![]() 为等比数列;
为等比数列;
(2)已知数列![]() 的前
的前![]() 项分别为
项分别为![]() .
.
①求数列![]() 和
和![]() 的通项公式;
的通项公式;
②是否存在元素均为正整数的集合![]() ,使得数列
,使得数列![]() 等差数列?证明你的结论.
等差数列?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com