
【题目】已知数列![]() 满足
满足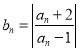 ,其中
,其中![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表达式(不必写出证明过程);
的表达式(不必写出证明过程);
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() .
.
(B)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表达式(不必写出证明过程);
的表达式(不必写出证明过程);
(2)设![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(A)(1)详见解析;(2)详见解析. (B)(1)详见解析;(2)![]() .
.
【解析】试题分析:(A)(1)利用![]() 的递推关系得到
的递推关系得到![]() ,从而求得
,从而求得![]() ,由此猜想
,由此猜想![]() .(2)将
.(2)将![]() 的表达式代入
的表达式代入![]() ,求得
,求得![]() ,用裂项求和法求得前
,用裂项求和法求得前![]() 项和
项和![]() .(B)利用
.(B)利用![]() ,和
,和![]() 的递推关系,可求得
的递推关系,可求得![]() 的值,由此猜想
的值,由此猜想![]() .(2)利用
.(2)利用![]() ,可求得
,可求得![]() 的通项公式,代入
的通项公式,代入![]() 并化简,利用基本不等式可求得其最大值.
并化简,利用基本不等式可求得其最大值.
试题解析:
(A)解(1)由题意, ![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
,
猜想得: ![]() .
.
(2)由(1)得![]() ,
,
则![]()
![]() .
.
(B)解(1)![]() ,
,
由![]() ,得
,得![]() ,
,
同理可得![]() ,
, ![]() ,
,
猜想: ![]() .
.
(2)由(1),![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() 满足止式,
满足止式,
所以![]() ,
,
则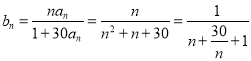 ,
, ![]() ,
,
设![]() ,则有
,则有![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
因为![]() ,且
,且![]() ,
,
所以当![]() 或
或![]() 时,
时, ![]() 有最大值
有最大值![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
| 6 |
| 7 | |
| 6 | 7 | 8 | |
| 5 | 6 | 7 | 8 |
(1)试估计![]() 班学生人数;
班学生人数;
(2)从![]() 班和
班和![]() 班抽出来的学生中各选一名,记
班抽出来的学生中各选一名,记![]() 班选出的学生为甲,
班选出的学生为甲,![]() 班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.
班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,短轴两个端点为
,短轴两个端点为![]() ,且四边形
,且四边形![]() 是边长为2的正方形.
是边长为2的正方形.
(1)求椭圆的方程;
(2)若![]() 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点![]() 满足
满足![]() ,连结
,连结![]() ,交椭圆于点
,交椭圆于点![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)在(2)的条件下,试问![]() 轴上是否存在异于点
轴上是否存在异于点![]() 的定点
的定点![]() ,使得以
,使得以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() 的交点,若存在,求出点
的交点,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量a=(cos α,sin α),b=(cos β,sin β),c=(-1,0).
(1) 求向量b+c的模的最大值;
(2) 若α=![]() ,且a⊥(b+c),求cos β的值.
,且a⊥(b+c),求cos β的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数, ![]() 是自然对数的底数),曲线
是自然对数的底数),曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]() .
.
(1)求![]() 的值;(2)求
的值;(2)求![]() 的单调区间;
的单调区间;
(3)设![]() (其中
(其中![]() 为
为![]() 的导函数)。证明:对任意
的导函数)。证明:对任意![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(ax2-x+1)(a>0,a≠1).
(1) 若a=![]() ,求函数f(x)的值域.
,求函数f(x)的值域.
(2) 当f(x)在区间![]() 上为增函数时,求a的取值范围.
上为增函数时,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:某污水处理厂要在一个矩形污水处理池(![]() )的池底水平铺设污水净化管道(
)的池底水平铺设污水净化管道(![]() 是直角顶点)来处理污水,管道越长污水净化效果越好,设计要求管道的的接口
是直角顶点)来处理污水,管道越长污水净化效果越好,设计要求管道的的接口![]() 是
是![]() 的中点,
的中点,![]() 分别落在线段
分别落在线段![]() 上。已知
上。已知![]() 米,
米,![]() 米,记
米,记![]() .
.
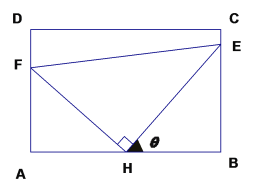
(1)试将污水净化管道的长度![]() 表示为
表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)若![]() ,求此时管道的长度
,求此时管道的长度![]() ;
;
(3)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度。
取何值时,污水净化效果最好?并求出此时管道的长度。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏,将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
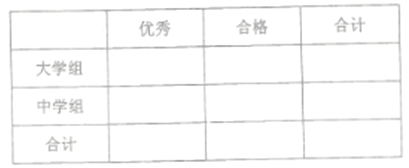
(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的![]() 列联表,并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
列联表,并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?


(2)若参赛选手共6万人,用频率估计概率,试估计其中优秀等级的选手人数;
(3)在优秀等级的选手中取6名,依次编号为1,2,3,4,5,6,在良好等级的选手中取6名,依次编号为1,2,3,4,5,6,在选出的6名优秀等级的选手中任取一名,记其编号为![]() ,在选出的6名良好等级的选手中任取一名,记其编号为
,在选出的6名良好等级的选手中任取一名,记其编号为![]() ,求使得方程组
,求使得方程组![]() 有唯一一组实数解
有唯一一组实数解![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在研究性学习中,关于三角形与三角函数知识的应用(约定三内角![]() 所对的边分别是
所对的边分别是![]() )得出如下一些结论:
)得出如下一些结论:
(1)若![]() 是钝角三角形,则
是钝角三角形,则![]() ;
;
(2)若![]() 是锐角三角形,则
是锐角三角形,则![]() ;
;
(3)在三角形![]() 中,若
中,若![]() ,则
,则![]()
(4)在![]() 中,若
中,若![]() ,则
,则![]()
其中错误命题的个数是 ( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com