
| A. | a>b>c | B. | c>a>b | C. | c>b>a | D. | a>c>b |
分析 f(x)=f(-x),函数f(x)是偶函数,可得函数F(x)=xf(x)是奇函数.由当x∈(-∞,0]时,F'(x)<0成立,可得函数F(x)在x∈(-∞,0]时单调递减,因此函数F(x)在x∈R上单调递减.
解答 解:∵f(x)=f(-x),函数f(x)是偶函数,∴函数F(x)=xf(x)是奇函数.
∵当x∈(-∞,0]时,F'(x)<0成立,∴函数F(x)在x∈(-∞,0]时单调递减,
因此函数F(x)在x∈R上单调递减.
∵20.1>1,ln2∈(0,1),$lo{g}_{2}\frac{1}{8}$<0,$a={2^{0.1}}•f({{2^{0.1}}}),b=ln2•f({ln2}),c={log_2}\frac{1}{8}•f({{{log}_2}\frac{1}{8}})$,
∴a<b<c.
故选:C.
点评 本题考查了函数的奇偶性、单调性、指数函数与对数函数的单调性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
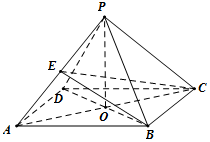 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,AC∩BD=O.
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,AC∩BD=O.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com