
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 是平行四边形,
是平行四边形, ![]() 且
且![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.
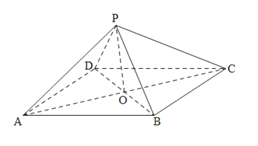
(1)![]() 为棱
为棱![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)求证: 平面![]() 平面
平面![]() ;
;
(3)若![]() ,
, ![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)由四边形![]() 是平行四边形,可得
是平行四边形,可得![]() 为
为![]() 中点,又
中点,又![]() 为
为![]() 中点,由三角形中位数定理可得
中点,由三角形中位数定理可得![]() ,再由线面平行的判定可得
,再由线面平行的判定可得![]() 平面
平面![]() ;(2)由
;(2)由![]() 平面
平面![]() ,得
,得![]() ,再由
,再由![]() ,可得
,可得![]() 平面
平面![]() ,进一步得到平面
,进一步得到平面![]() 平面
平面![]() ;(3)由已知求出四边形
;(3)由已知求出四边形![]() 的面积,先求出高
的面积,先求出高![]() ,再由棱锥的体积公式得答案.
,再由棱锥的体积公式得答案.
试题解析:(1)因为点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,
的中点,
所以![]()
![]() ,又因为
,又因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)证明:因为![]() 平面
平面![]() ,又
,又![]() 平面
平面![]()
所以![]() ,又因为
,又因为![]() ,
,
所以![]() 平面
平面![]() ,又因为
,又因为![]() 平面
平面![]() .
.
所以平面![]() 平面
平面![]() .
.
(3)因为![]() ,又
,又![]() ,
,
所以四边形![]() 的面积为4,
的面积为4,
因为![]() ,点
,点![]() 为
为![]() 的中点,
的中点,
所以![]() .
.
所以四棱锥![]() 的体积为:
的体积为: ![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、面面垂直的判定定理以及棱锥的体积公式,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


科目:高中数学 来源: 题型:
【题目】已知函数![]() =
=
(1)写出该函数的单调区间;
(2)若函数![]() =
=![]() -m恰有3个不同零点,求实数m的取值范围;
-m恰有3个不同零点,求实数m的取值范围;
(3)若![]() ≤n2-2bn+1对所有x∈[-1,1],b∈[-1,1]恒成立,求实数n的取值范围.
≤n2-2bn+1对所有x∈[-1,1],b∈[-1,1]恒成立,求实数n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查表明,市民对城市的居住满意度与该城市环境质量、城市建设、物价与收入的满意度有极强的相关性,现将这三项的满意度指标分别记为x、y、z,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意,再用综合指标ω=x+y+z的值评定居民对城市的居住满意度等级:若ω≥4,则居住满意度为一级;若2≤ω≤3,则居住满意度为二级;若0≤ω≤1,则居住满意度为三级,为了解某城市居民对该城市的居住满意度,研究人员从此城市居民中随机抽取10人进行调查,得到如下结果:
人员编号 | 1 | 2 | 3 | 4 | 5 |
(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,1,1) | (1,2,1) |
人员编号 | 6 | 7 | 8 | 9 | 10 |
(x,y,z) | (1,2,2) | (1,1,1) | (1,2,2) | (1,0,0) | (1,1,1) |
(1)在这10名被调查者中任取两人,求这两人的居住满意度指标z相同的概率;
(2)从居住满意度为一级的被调查者中随机抽取一人,其综合指标为m,从居住满意度不是一级的被调查者中任取一人,其综合指标为n,记随机变量ξ=m﹣n,求随机变量ξ的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 的值域为[0,+∞),求实数a的取值范围;
的值域为[0,+∞),求实数a的取值范围;
(2)若关于x的不等式F(x)>af(x)+12恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:如图,梯形ABCD中,AD∥BC,∠C= ![]() ,以AB为直径的⊙O恰与CD相切于点E,⊙O交BC于F,连结EF.
,以AB为直径的⊙O恰与CD相切于点E,⊙O交BC于F,连结EF. 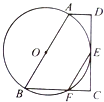
(1)求证:AD+BC=AB;
(2)求证:EF是AD与AB的等比中项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,短轴右端点为
,短轴右端点为![]() ,
, ![]() 为线段
为线段![]() 的中点.
的中点.
(Ⅰ) 求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 任作一条直线与椭圆
任作一条直线与椭圆![]() 相交于两点
相交于两点![]() ,试探究在
,试探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x+1)2ex , 设k∈[﹣3,﹣1],对任意x1 , x2∈[k,k+2],则|f(x1)﹣f(x2)|的最大值为( )
A.4e﹣3
B.4e
C.4e+e﹣3
D.4e+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com