
����Ŀ���������������Գ��еľ�ס�������ó��л������������н��衢����������������м�ǿ������ԣ��ֽ�������������ָ��ֱ��Ϊx��y��z���������ǽ���������0��ʾ�����⣬1��ʾ�������⣬2��ʾ���⣬�����ۺ�ָ���=x+y+z��ֵ��������Գ��еľ�ס����ȵȼ������ء�4�����ס�����Ϊһ������2�ܦء�3�����ס�����Ϊ��������0�ܦء�1�����ס�����Ϊ������Ϊ�˽�ij���о���Ըó��еľ�ס����ȣ��о���Ա�Ӵ˳��о����������ȡ10�˽��е��飬�õ����½����
��Ա��� | 1 | 2 | 3 | 4 | 5 |
��x��y��z�� | ��1��1��2�� | ��2��1��1�� | ��2��2��2�� | ��0��1��1�� | ��1��2��1�� |
��Ա��� | 6 | 7 | 8 | 9 | 10 |
��x��y��z�� | ��1��2��2�� | ��1��1��1�� | ��1��2��2�� | ��1��0��0�� | ��1��1��1�� |
��1������10��������������ȡ���ˣ��������˵ľ�ס�����ָ��z��ͬ�ĸ��ʣ�
��2���Ӿ�ס�����Ϊһ���ı��������������ȡһ�ˣ����ۺ�ָ��Ϊm���Ӿ�ס����Ȳ���һ���ı�����������ȡһ�ˣ����ۺ�ָ��Ϊn�������������=m��n������������εķֲ��м�����ѧ������
���𰸡�
��1���⣺���¼�AΪ����10������������ȡ���ˣ������˵ľ�ס�����ָ��z��ͬ����
���ס����ָ��zΪ0��ֻ�б��Ϊ9��һλ��
��ס����ָ��zΪ1���б��Ϊ2��4��5��7��10������λ��
��ס����ָ��zΪ2���б��Ϊ1��3��6��8������λ��
��10������������ȡ���ˣ������¼�����n= ![]() =10��
=10��
�����˵ľ�ס�����ָ��z��ͬ�Ľ��Ϊ ![]() =16��
=16��
�������˵ľ�ס�����ָ��z��ͬ�ĸ���p= ![]() ��
��
��2���⣺����10���������ߵ��ۺ�ָ�꣬�����±���
��Ա��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
�ۺ�ָ�� | 4 | 4 | 6 | 2 | 4 | 5 | 3 | 5 | 1 | 3 |
���о�ס�����Ϊһ�����б��Ϊ1��2��3��5��6��8����λ����m�Ŀ���ȡֵΪ4��5��6��
��ס����Ȳ���һ�����б��Ϊ4��7��9��10����λ����n�Ŀ���ȡֵΪ1��2��3��
���=m��n�Ŀ���ȡֵΪ1��2��3��4��5��
P����=1��= ![]() =
= ![]() ��
��
P����=2��= ![]() =
= ![]() ��
��
P����=3��= ![]() =
= ![]() ��
��
P����=4��= ![]() =
= ![]() ��
��
P����=5��= ![]() =
= ![]() ��
��
��εķֲ���Ϊ��
�� | 1 | 2 | p>3 | 4 | 5 |
P |
|
|
|
|
|
E��= ![]() =
= ![]()
����������1�����¼�AΪ����10������������ȡ���ˣ������˵ľ�ס�����ָ��z��ͬ������10������������ȡ���ˣ�����������¼�����������������˵ľ�ס�����ָ��z��ͬ�Ľ�����ɴ�����������˵ľ�ס�����ָ��z��ͬ�ĸ��ʣ���2���������=m��n�Ŀ���ȡֵΪ1��2��3��4��5���ֱ������Ӧ�ĸ��ʣ��ɴ�������εķֲ��к�E�Σ�
�����㾫����������Ĺؼ�����������ɢ�������������ֲ��е����֪ʶ���������������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������![]() �У�
�� ![]() ��
�� ![]() ��
�� ![]() ��ֱ������
��ֱ������![]() ͨ��ֱ������
ͨ��ֱ������![]() ��ֱ��
��ֱ��![]() Ϊ����ת�õ�����ʹ��ƽ��
Ϊ����ת�õ�����ʹ��ƽ��![]() ƽ��
ƽ��![]() ��
�� ![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬
���е㣬 ![]() Ϊ�߶�
Ϊ�߶�![]() �ϵĶ��㣮
�ϵĶ��㣮

��![]() ����֤��
����֤�� ![]() ��
��
��![]() ������
������![]() ����
����![]() ʱ����֤��ֱ��
ʱ����֤��ֱ��![]() ƽ��
ƽ��![]() ��
��
��![]() ������
������![]() ���߶�
���߶�![]() �е�ʱ����ֱ��
�е�ʱ����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|2x��1|+|2x+a|��g��x��=x+3��
��1����a=��2ʱ����ʽf��x����g��x���Ľ⼯��
��2����a����1���ҵ� ![]() ʱ��f��x����g��x������a��ȡֵ��Χ��
ʱ��f��x����g��x������a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2��ex+e��x������2x+1��2��e2x+1+e��2x��1����������f��x����0��ʵ��x��ȡֵ��ΧΪ�� ��
A.����1���� ![]() ��
��
B.�����ޣ���1��
C.���� ![]() ��+�ޣ�
��+�ޣ�
D.�����ޣ���1���ȣ��� ![]() ��+�ޣ�
��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�����п���ʽ�����˲ţ��涨������![]() ������������������ѡȡ�������в��ԣ��������������Ե㶼���Ժϸ���ɲμ�����,����¼��,��֪������ÿ�����������Խ������Ӱ��,������С���С��һ��ǰ���μ��п�,С���ڲ��Ե�
������������������ѡȡ�������в��ԣ��������������Ե㶼���Ժϸ���ɲμ�����,����¼��,��֪������ÿ�����������Խ������Ӱ��,������С���С��һ��ǰ���μ��п�,С���ڲ��Ե�![]() ���Ժϸ�����ʷֱ�Ϊ
���Ժϸ�����ʷֱ�Ϊ![]() ,С���������������Ե�����ϸ�����ʶ���
,С���������������Ե�����ϸ�����ʶ���![]() .
.
��1����С��ѡ�����������Ե���Բ���ʹ�ÿ��Բμ����ԵĿ������������˵������;
��2������С��ѡ�����Ե�![]() ���в��ԣ�С��ѡ����Ե�
���в��ԣ�С��ѡ����Ե�![]() ���в���,��
���в���,��![]() Ϊ�����ڸ����Ե���Ժϸ�IJ��Ե����֮��,����������
Ϊ�����ڸ����Ե���Ժϸ�IJ��Ե����֮��,����������![]() �ķֲ��м���ѧ����
�ķֲ��м���ѧ����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڣ�0��+�����ĺ���f��x��������������������
�ٶ���������ʵ��a��b������f��ab��=f��a��+f��b��-1��
��f��2��=0��
��x��1ʱ������f��x����1��
��1����f��1����![]() ��ֵ��
��ֵ��
��2����֤������f��x���ڣ�0��+�������Ǽ�������
��3�������������k��ʹ����x�ķ���f��kx��+f��2-x��=-1�н⣬����ʵ��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������![]() �У��ı���
�У��ı���![]() ��ƽ���ı���,
��ƽ���ı���, ![]() ��
��![]() ,
, ![]() ,
, ![]() ƽ��
ƽ��![]() .
.
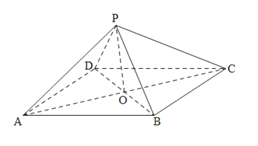
��1��![]() ��
Ϊ��![]() ���е�,��֤:
���е�,��֤: ![]() ƽ��
ƽ��![]() ��
��
��2����֤: ƽ��![]() ƽ��
ƽ��![]() ��
��
��3����![]() ,
, ![]() ,������
,������![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ΪR�ĺ���f��x��=![]() ���溯����
���溯����
��1����ʵ��a��b��ֵ��
��2���жϲ��ö���֤��f��x���ڣ�-�ޣ�+�����ϵĵ����ԣ�
��3�����������x��[1��2]������t��[1��2]ʹ�ò���ʽf��x2+tx��+f��2x+m����0��������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ�У���ԭ��Ϊ���㣬 ![]() ���������Ϊ���Ὠ��������ϵ����֪����
���������Ϊ���Ὠ��������ϵ����֪����![]() ��
�� ![]() ����֪����
����֪����![]() ��ֱ��
��ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ ��
��![]() Ϊ��������ֱ��
Ϊ��������ֱ��![]() ������
������![]() �ֱ���
�ֱ���![]() ��
��![]() ����.
����.
��1��д������![]() ��ֱ��
��ֱ��![]() ��ֱ�����귽��.
��ֱ�����귽��.
��2����![]() ��
�� ![]() ��
�� ![]() �ɵȱ����У���
�ɵȱ����У���![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com