
分析 (1)首先利用三角函数的恒等变换把函数的关系式变性成正弦型函数,进一步求出函数的值.
(2)利用正弦型函数的解析式,进一步利用函数的定义域求出函数的值域,最后利用整体思想求出函数的单调区间.
解答 解:(1)$f(x)=sin(2x+\frac{π}{4})+cos(2x-\frac{π}{4})$
=2($\frac{\sqrt{2}}{2}sin2x+\frac{\sqrt{2}}{2}cos2x$)
=2sin(2x+$\frac{π}{4}$),
所以:f($\frac{π}{2}$)=2sin(π+$\frac{π}{4}$)=-$\sqrt{2}$.
(2)由于:x∈R,且f(x)=2sin(2x+$\frac{π}{4}$),
所以函数的值域为:f(x)∈[-2,2].
令:$-\frac{π}{2}+2kπ≤2x+\frac{π}{4}≤2kπ+\frac{π}{2}$
整理得:$-\frac{3π}{8}+kπ≤x≤kπ+\frac{π}{8}$,(k∈Z)
所以函数的单调递增区间为:[$-\frac{3π}{8}+kπ,kπ+\frac{π}{8}$](k∈Z)
点评 本题考查的知识要点:三角函数的关系式的恒等变换,利用正弦型函数的定义域求函数的值域,利用整体思想求函数的单调区间.主要考查学生的应用能力.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 70 | B. | 64 | C. | 48 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
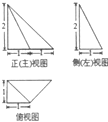
| A. | $\frac{{9+2\sqrt{3}+\sqrt{5}}}{2}$ | B. | $\frac{{9+2\sqrt{3}}}{2}$ | C. | $\frac{{9+2\sqrt{5}}}{2}$ | D. | $\frac{{11+\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com