
分析 (1)利用配方法得到圆的标准方程,根据直线垂直的条件:斜率之积为-1,点与圆的位置关系即可求出a的取值范围;
(2)求出A,B的坐标,利用$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,求出a,即可求圆C的方程.
解答 解:(1)圆的标准方程为(x+1)2+(y-2)2=5-a,
则圆心C(-1,2),半径r=$\sqrt{5-a}$,
∵弦AB的中点为M(0,1).
∴点M在圆内部,即(0+1)2+(1-2)2<5-a,
∴5-a>2,即a<3.
∵弦的中点为M(0,1).
∴直线CM的斜率k=$\frac{2-1}{-1-0}$=-1,
则直线l的斜率k=1,
则直线l的方程为y-1=x,即x-y+1=0;
(2)由圆C:x2+y2+2x-4y+a=0,与x-y+1=0联立得2x2+a-3=0,故x=±$\sqrt{\frac{3-a}{2}}$.
不妨设$A(\sqrt{\frac{3-a}{2}},\sqrt{\frac{3-a}{2}}+1)$,$B(-\sqrt{\frac{3-a}{2}},-\sqrt{\frac{3-a}{2}}+1)$…(7分)
则$\overrightarrow{OA}•\overrightarrow{OB}=-\frac{3-a}{2}+1-\frac{3-a}{2}=a-2=0$,故a=2…(9分)
故圆C:x2+y2+2x-4y+2=0…(10分)
点评 本题主要考查直线和圆的方程的应用,同时考查向量知识的运用,利用配方法将圆配成标准方程是解决本题的关键.


科目:高中数学 来源: 题型:选择题
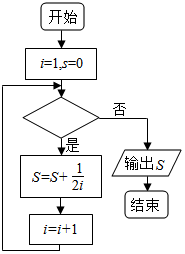
| A. | i≤1007 | B. | i≤1008 | C. | i>1008 | D. | i>1007 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-2y-3=0 | B. | 3x-2y+3=0 | C. | 2x-3y-3=0 | D. | 2x-3y+3=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
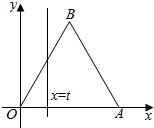 如图,△OAB是边长为2的正三角形,当一条垂直于底边OA(垂足不与O,A重合)的直线x=t从左至右移动时,直线l把三角形分成两部分,记直线l左边部分的面积y.
如图,△OAB是边长为2的正三角形,当一条垂直于底边OA(垂足不与O,A重合)的直线x=t从左至右移动时,直线l把三角形分成两部分,记直线l左边部分的面积y.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {1,3,5} | C. | {1,3,6,7} | D. | {1,3,5,7} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com