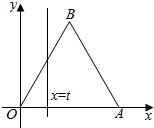Question

5．如图，△OAB是边长为2的正三角形，当一条垂直于底边OA（垂足不与O，A重合）的直线x=t从左至右移动时，直线l把三角形分成两部分，记直线l左边部分的面积y．
（Ⅰ）写出函数y=f（t）的解析式；
（Ⅱ）写出函数y=f（t）的定义域和值域．

Answer 1

分析 （Ⅰ）结合图形，便可看出分0＜t≤1和1＜t＜2两种情况来求直线x=t的左边图形的面积，然后用分段函数写出y=f（t）的解析式即可；
（Ⅱ）可求出OAB的面积，根据题意即可写出函数y=f（t）的定义域和值域．

解答 解：（Ⅰ）（1）当0＜t≤1时，$y=\frac{1}{2}•t•t•tan60°=\frac{\sqrt{3}}{2}{t}^{2}$；
（2）当1＜t＜2时，$y=\frac{1}{2}•2•2•sin60°-\frac{1}{2}•（2-t）•（2-t）•tan60°$$\sqrt{3}-\frac{\sqrt{3}}{2}（4-4t+{t}^{2}）=-\frac{\sqrt{3}}{2}{t}^{2}+2\sqrt{3}t-\sqrt{3}$；
∴$f（t）=\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}{t}^{2}}&{0＜t≤1}\\{-\frac{\sqrt{3}}{2}{t}^{2}+2\sqrt{3}t-\sqrt{3}}&{1＜t＜2}\end{array}\right.$；
（Ⅱ）y=f（x）的定义域为（0，2）；
${S}_{△OAB}=\sqrt{3}$，∴由问题的实际知，y=f（x）的值域为（0，$\sqrt{3}$）．

点评 考查三角形的面积公式，数形结合解题的方法，分段函数的定义及表示形式，根据实际问题求函数的定义域和值域的方法．