
| A. | $|{\vec a}|=\frac{{\sqrt{3}}}{2}$ | B. | $|{\vec b}|=\frac{1}{2}$ | C. | $({\vec a+\vec b})•\vec a=-\frac{1}{4}$ | D. | $\vec a⊥\vec b$ |
分析 可作图,取BC边的中点D,并连接AD,从而可以得出$\overrightarrow{AD}=\overrightarrow{a}$,$\overrightarrow{CB}=2\overrightarrow{b}$,从而有$\overrightarrow{a}⊥\overrightarrow{b}$,这样即可求出$|\overrightarrow{a}|,|\overrightarrow{b}|$和$(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{a}$的值,从而便可找出错误的结论.
解答 解:A.如图,设边BC的中点为D,则: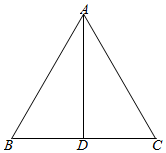
$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{a}=2\overrightarrow{AD}$,$|\overrightarrow{AD}|=\frac{\sqrt{3}}{2}$;
∴$|\overrightarrow{a}|=\frac{\sqrt{3}}{2}$,∴该选项正确;
B.∵$\overrightarrow{AB}-\overrightarrow{AC}=2\overrightarrow b=\overrightarrow{CB,}|{\overrightarrow{CB}}|=1$,∴$|{\overrightarrow b}|=\frac{1}{2}$,∴该选项正确;
C.$\overrightarrow{AD}=\overrightarrow{a},\overrightarrow{AB}=\overrightarrow{a}+\overrightarrow{b}$;
∴$(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{a}=\overrightarrow{AB}•\overrightarrow{AD}=1•\frac{\sqrt{3}}{2}•\frac{\sqrt{3}}{2}=\frac{3}{4}$,∴该选项错误;
D.AD⊥BC,由前面$\overrightarrow{AD}=\overrightarrow{a},\overrightarrow{CB}=2\overrightarrow{b}$,∴$\overrightarrow{a}⊥(2\overrightarrow{b})$,即$\overrightarrow{a}⊥\overrightarrow{b}$,∴该选项正确.
故选:C.
点评 考查向量加法的平行四边形法则,向量的数乘运算,以及数量积的计算公式,余弦函数的定义,向量数乘的几何意义,向量垂直的概念.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 项目/学号编号 | ① | ② | ③ | ④ | ⑤ |
| (1) | T | T | T | ||
| (2) | T | T | T | ||
| (3) | T | T | T | T | |
| (4) | T | T | T | ||
| (5) | T | T | T | T | |
| (6) | T | T | T | ||
| (7) | T | T | T | T | |
| (8) | T | T | T | T | T |
| (9) | T | T | T | ||
| (10) | T | T | T | T | T |
| 注:“T”表示合格,空白表示不合格 | |||||
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
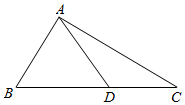 如图,D是直角△ABC斜边BC上一点,AC=$\sqrt{3}$DC.
如图,D是直角△ABC斜边BC上一点,AC=$\sqrt{3}$DC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $-\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $-\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com