
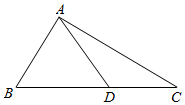
 如图,D是直角△ABC斜边BC上一点,AC=$\sqrt{3}$DC.
如图,D是直角△ABC斜边BC上一点,AC=$\sqrt{3}$DC.分析 (Ⅰ)由正弦定理有$\frac{AC}{sin∠ADC}=\frac{DC}{sin∠DAC}$,又$AC=\sqrt{3}DC$,可得$sin∠ADC=\sqrt{3}sin∠DAC=\frac{{\sqrt{3}}}{2}$,结合∠ADC=∠B+∠BAD=∠B+60°>60°,可求∠ADC,即可求B的值.
(Ⅱ)设DC=x,则BD=2x,BC=3x,$AC=\sqrt{3}x$,可求$sinB=\frac{AC}{BC}=\frac{{\sqrt{3}}}{3}$,$cosB=\frac{{\sqrt{6}}}{3}$,$AB=\sqrt{6}x$,由余弦定理即可计算得解DC的长.
解答  (本题满分为12分)
(本题满分为12分)
解:(Ⅰ)在△ABC中,根据正弦定理,有$\frac{AC}{sin∠ADC}=\frac{DC}{sin∠DAC}$.
因为$AC=\sqrt{3}DC$,所以$sin∠ADC=\sqrt{3}sin∠DAC=\frac{{\sqrt{3}}}{2}$.
又∠ADC=∠B+∠BAD=∠B+60°>60°,
所以∠ADC=120°.…(3分
于是∠C=180°-120°-30°=30°,所以∠B=60°.…(6分)
(Ⅱ)设DC=x,则BD=2x,BC=3x,$AC=\sqrt{3}x$.
于是$sinB=\frac{AC}{BC}=\frac{{\sqrt{3}}}{3}$,$cosB=\frac{{\sqrt{6}}}{3}$,$AB=\sqrt{6}x$.…(9分)
在△ABD中,由余弦定理,得 AD2=AB2+BD2-2AB•BDcosB,
即${(2\sqrt{2})^2}=6{x^2}+4{x^2}-2×\sqrt{6}x×2x×\frac{{\sqrt{6}}}{3}=2{x^2}$,得x=2.
故DC=2.…(12分)
点评 本题主要考查了正弦定理,余弦定理,三角形内角和定理在解三角形中的应用,考查了计算能力和转化思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年入流量 | 40<X<80 | 80≤X≤120 | X>120 |
| 年数 | 10 | 35 | 5 |
| 年入流量 | 40<X<80 | 80≤X≤120 | X>120 |
| 最多运行台数 | 1 | 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {1,2,3} | C. | {1,2} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $|{\vec a}|=\frac{{\sqrt{3}}}{2}$ | B. | $|{\vec b}|=\frac{1}{2}$ | C. | $({\vec a+\vec b})•\vec a=-\frac{1}{4}$ | D. | $\vec a⊥\vec b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -10 | C. | 4 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com