
分析 对x分x<1,1≤x≤4与x>4范围的讨论,去掉原不等式左端的绝对值符号,从而易解不等式|x-1|+|x-4|≤2的解集.
解答 解:当x<1时,|x-1|+|x-4|≤2?-x+1+4-x≤2,
解得:x≥$\frac{3}{2}$;
当1≤x≤4时,|x-1|+|x-4|≤2?x-1+4-x=3≤2,不成立;
当x>4时,|x-1|+|x-4|≤2?x-1+x-4=2x-5≤2,
解得:x≤$\frac{7}{2}$.
综上所述,不等式|x-1|+|x-4|≤2的解集为∅,
故答案为:∅.
点评 本题考查绝对值不等式的解法,去掉绝对值符号是关键,考查分类讨论思想与运算求解能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 0≤a≤1 | B. | a≤1 | C. | a<1 | D. | 0<a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
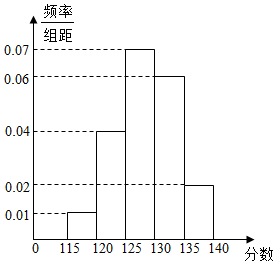 某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.
某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.| 区间 | 人数 |
| [115,120) | 25 |
| [120,125) | a |
| [125,130) | 175 |
| [130,135) | 150 |
| [135,140) | b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | -3 | C. | 3 | D. | $\frac{4}{{5}_{\;}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数区间 | 甲班频率 | 乙班频率 |
| [0,30) | 0.1 | 0.2 |
| [30,60) | 0.2 | 0.2 |
| [60,90) | 0.3 | 0.3 |
| [90,120) | 0.2 | 0.2 |
| [120,150) | 0.2 | 0.1 |
| 优秀 | 不优秀 | 总计 | |
| 甲班 | |||
| 乙班 | |||
| 总计 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
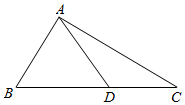 如图,D是直角△ABC斜边BC上一点,AC=$\sqrt{3}$DC.
如图,D是直角△ABC斜边BC上一点,AC=$\sqrt{3}$DC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com