
| 年入流量 | 40<X<80 | 80≤X≤120 | X>120 |
| 年数 | 10 | 35 | 5 |
| 年入流量 | 40<X<80 | 80≤X≤120 | X>120 |
| 最多运行台数 | 1 | 2 | 3 |
分析 (1)依题意,先求出随机变量Y的分布列,由此能求出随机变量Y的数学期望.
(2)记水电站总利润为Z(单位:万元),分别求出安装1台发电机、?安装2台发电机、?安装3台发电机的利润的期望,由此得到欲使水电站年总利润的期望达到最大,应安装发电机2台.
解答 解:(1)依题意,${p_1}=p(40<X<80)=\frac{10}{50}=0.2$.
${p_2}=p(80≤X≤120)=\frac{35}{50}=0.7$,
${p_3}=p(X≥120)=\frac{5}{50}=0.1$.
随机变量Y的分布列为
| Y | 1 | 2 | 3 |
| P | 0.2 | 0.7 | 0.1 |
| Z | 4200 | 10000 |
| P | 0.2 | 0.8 |
| Z | 40<X<80 | 80≤X≤120 | X>120 |
| P | 0.2 | 0.7 | 0.1 |
点评 本题考查离散型机量的分布和数学期望的求法及应用,正确理解题意是基础,准确写出各分布列是关键.本题考查学生逻辑推理能力和离散随机变量的分布.


科目:高中数学 来源: 题型:解答题
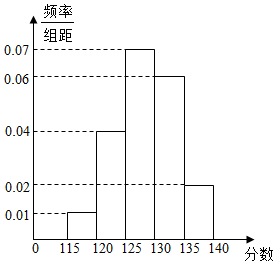 某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.
某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.| 区间 | 人数 |
| [115,120) | 25 |
| [120,125) | a |
| [125,130) | 175 |
| [130,135) | 150 |
| [135,140) | b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数区间 | 甲班频率 | 乙班频率 |
| [0,30) | 0.1 | 0.2 |
| [30,60) | 0.2 | 0.2 |
| [60,90) | 0.3 | 0.3 |
| [90,120) | 0.2 | 0.2 |
| [120,150) | 0.2 | 0.1 |
| 优秀 | 不优秀 | 总计 | |
| 甲班 | |||
| 乙班 | |||
| 总计 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 项目/学号编号 | ① | ② | ③ | ④ | ⑤ |
| (1) | T | T | T | ||
| (2) | T | T | T | ||
| (3) | T | T | T | T | |
| (4) | T | T | T | ||
| (5) | T | T | T | T | |
| (6) | T | T | T | ||
| (7) | T | T | T | T | |
| (8) | T | T | T | T | T |
| (9) | T | T | T | ||
| (10) | T | T | T | T | T |
| 注:“T”表示合格,空白表示不合格 | |||||
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
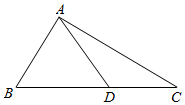 如图,D是直角△ABC斜边BC上一点,AC=$\sqrt{3}$DC.
如图,D是直角△ABC斜边BC上一点,AC=$\sqrt{3}$DC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $-\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $-\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com