
分析 画出约束条件的可行域,化简所求表达式,利用表达式的几何意义,求解即可.
解答 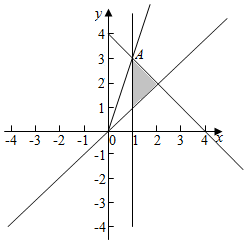 解:x,y满足约束条件$\left\{{\begin{array}{l}{x-1≥0}\\{x-y<0}\\{x+y-4≤0}\end{array}}\right.$的可行域如图:
解:x,y满足约束条件$\left\{{\begin{array}{l}{x-1≥0}\\{x-y<0}\\{x+y-4≤0}\end{array}}\right.$的可行域如图:
则$\frac{x+2y}{2x+y}$=$\frac{x+\frac{1}{2}y+\frac{3}{2}y}{2x+y}$=$\frac{1}{2}$+$\frac{3}{4\frac{x}{y}+2}$.
由可行域可知:$\frac{y}{x}$∈[1,kOA],由$\left\{\begin{array}{l}{x-1=0}\\{x+y-4=0}\end{array}\right.$,可得A(1,3),
kOA=3,
$\frac{4x}{y}$∈$[\frac{4}{3},4]$,$\frac{4x}{y}$+2∈$[\frac{10}{3},6]$,
$\frac{3}{4\frac{x}{y}+2}$∈$[\frac{1}{2},\frac{9}{10}]$,
则$\frac{x+2y}{2x+y}$∈[1,$\frac{7}{5}$].
故答案为:[1,$\frac{7}{5}$].
点评 本题考查了利用线性规划求目标函数的值域,一般分两步进行:1、根据不等式组,作出不等式组表示的平面区域;2、由目标函数的特点及几何意义,利用数形结合思想,转化为图形之间的关系问题求解.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
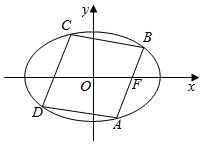 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F(c,0),菱形ABCD的各顶点在椭圆E上,且直线AB经过点F.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F(c,0),菱形ABCD的各顶点在椭圆E上,且直线AB经过点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin2x+cos2x | B. | $y=cos(2x+\frac{π}{2})$ | C. | y=cos(2x-1) | D. | y=cos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “a2>9”是“a>3”的充分不必要条件 | |
| B. | “?x0∈R,使得$sin{x_0}+\frac{2}{{sin{x_0}}}>2\sqrt{2}$”的否定是“$?x∈R,sinx+\frac{2}{sinx}<2\sqrt{2}$” | |
| C. | 若A∧B是假命题,则A∨B是假命题 | |
| D. | “若a<0,则x2+ax+a<0有解”的否命题为“若a≥0,则x2+ax+a<0无解” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限或x轴正半轴上 | B. | 第二象限或x轴负半轴上 | ||
| C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com