
【题目】如图,在六面体ABCDEFG中,平面![]() 平面DEFG,
平面DEFG,![]() 平面DEFC,
平面DEFC,![]() ,
,![]() ,且
,且![]() .
.
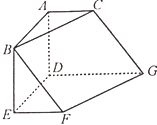
(1)求证:![]() 平面ACGD;
平面ACGD;
(2)若![]() ,求点D到平面GFBC的距离
,求点D到平面GFBC的距离
【答案】(1)证明见解析;(2)![]() .
.
【解析】
![]() 证明
证明![]() ,
,![]() ,得到
,得到![]() 平面DEFG,得到平面
平面DEFG,得到平面![]() 平面DEFG,取DG的中点为M,连接AM、FM,证明
平面DEFG,取DG的中点为M,连接AM、FM,证明![]() ,推出
,推出![]() 平面ACGD.
平面ACGD.
![]() 以DG、DE、DA为方向建立空间直角坐标系,求出平面BGF法向量,通过点D到平面
以DG、DE、DA为方向建立空间直角坐标系,求出平面BGF法向量,通过点D到平面![]() 即平面
即平面![]() 的距离,求解即可.
的距离,求解即可.
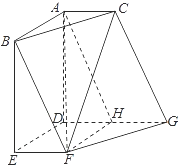
(1)证明:已知如图:
∵平面![]() 平面DEFG,平面
平面DEFG,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴ADEB为平行四边形,![]() .
.
∴![]() 平面DEFG,
平面DEFG,
∵![]() 平面BEF,
平面BEF,
∴平面![]() 平面DEFG.
平面DEFG.
取DG的中点为M,连接AM、FM,
则由已知条件易证四边形DEFM是平行四边形,
∴![]() ,
,
又∵![]() ,
,
∴![]()
∴四边形ABFM是平行四边形,即![]() ,
,
又![]() 平面ACGD,
平面ACGD,
故![]() 平面ACGD.
平面ACGD.
(2)由(1)得![]() 平面
平面![]() ,所以
,所以![]() ,
,
根据几何关系得:![]()
以DG、DE、DA为方向建立空间直角坐标系,如图
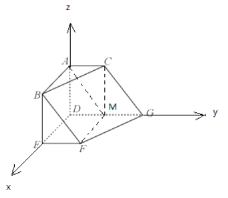
则![]() ,
,![]() ,
,![]()
所以![]() ,
,![]()
设平面![]() 法向量为
法向量为![]() ,
,
则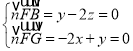 ,取
,取![]() 得
得![]()
所以点![]() 到平面
到平面![]() (即平面
(即平面![]() )的距离
)的距离
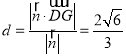 .
.


科目:高中数学 来源: 题型:
【题目】为比较甲、乙两名高中学生的数学素养,对课程标准中规定的数学六大素养进行指标测验(指标值满分为100分,分值高者为优),根据测验情况绘制了如图所示的六大素养指标雷达图,则下面叙述不正确的是( )
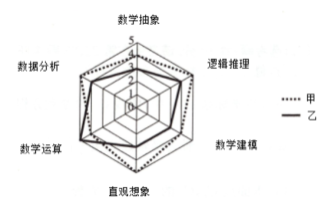
A.甲的数据分析素养优于乙B.乙的数据分析素养优于数学建模素养
C.甲的六大素养整体水平优于乙D.甲的六大素养中数学运算最强
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知圆F1:(x+1)2 +y2= r2(1≤r≤3),圆F2:(x-1)2+y2= (4-r)2.
(1)证明:圆F1与圆F2有公共点,并求公共点的轨迹E的方程;
(2)已知点Q(m,0)(m<0),过点E斜率为k(k≠0)的直线与(Ⅰ)中轨迹E相交于M,N两点,记直线QM的斜率为k1,直线QN的斜率为k2,是否存在实数m使得k(k1+k2)为定值?若存在,求出m的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() 在线段
在线段![]() 上,且
上,且![]() 。将
。将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到
到![]() 的位置(如图2所示),且
的位置(如图2所示),且![]() 。
。
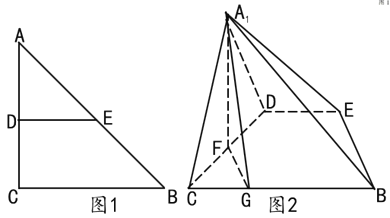
(1)证明:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于三次函数![]() ,给出定义:设
,给出定义:设![]() 是函数
是函数![]() 的导数,
的导数,![]() 是
是![]() 的导数,若方程
的导数,若方程![]() 有实数解
有实数解![]() ,则称点
,则称点![]() 为函数
为函数![]() 的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数
的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数![]() .
.
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年9月1日,《西安市生活垃圾分类管理办法》正式实施.根据规定,生活垃圾分为可回收物、有害垃圾、厨余垃圾和其他垃圾,个人和单位如果不按规定进行垃圾分类将面临罚款,并纳入征信系统.为调查市民对垃圾分类的了解程度,某调查小组随机抽取了某小区的100位市民,请他们指出生活中若干项常见垃圾的种类,把能准确分类不少于3项的称为“比较了解”,少于三项的称为“不太了解”.调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
男(人) | 1 | 5 | 15 | 8 | 6 | 7 | 3 |
女(人) | 0 | 4 | 11 | 13 | 10 | 12 | 5 |
(1)完成如下![]() 列联表并判断是否有99%的把握认为了解垃圾分类与性别有关?
列联表并判断是否有99%的把握认为了解垃圾分类与性别有关?
比较了解 | 不太了解 | 合计 | |
男 | |||
女 | |||
合计 |
(2)从对垃圾分类比较了解的市民中用分层抽样的方式抽取8位,现从这8位市民中随机选取两位,求至多有一位男市民的概率.
附: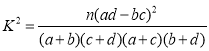
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com