
【题目】设x,y,z均为正实数,且xyz=1,求证: ![]() +
+ ![]() +
+ ![]() ≥xy+yz+zx.
≥xy+yz+zx.
科目:高中数学 来源: 题型:
【题目】已知集合M={(x,y)|y=f(x)},若对于任意实数对(x1 , y1)∈M,存在(x2 , y2)∈M,使x1x2+y1y2=0成立,则称集合M是“垂直对点集”,给出下列四个集合: ①M={(x,y)|y= ![]() };
};
②M={(x,y)|y=sinx+1};
③={(x,y)|y=2x﹣2};
④M={(x,y)|y=log2x}
其中是“垂直对点集”的序号是( )
A.②③④
B.①②④
C.①③④
D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一缉私艇巡航至距领海边界线l(一条南北方向的直线)3.8海里的A处,发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑,缉私艇立即追击,已知缉私艇的最大航速是走私船最大航速的3倍,假设缉私艇和走私船均按直线方向以最大航速航行. 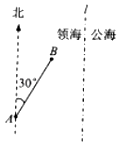
(1)若走私船沿正东方向逃离,试确定缉私艇的追击方向,使得用最短时间在领海内拦截成功;(参考数据:sin17°≈ ![]() ,
, ![]() ≈5.7446)
≈5.7446)
(2)问:无论走私船沿何方向逃跑,缉私艇是否总能在领海内成功拦截?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=asinωx+bcosωx(0<ω<5,ab≠0)的图象的一条对称轴方程是 ![]() ,函数f'(x)的图象的一个对称中心是
,函数f'(x)的图象的一个对称中心是 ![]() ,则f(x)的最小正周期是( )
,则f(x)的最小正周期是( )
A.![]()
B.![]()
C.π
D.2π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xex﹣a(lnx+x).
(1)若函数f(x)恒有两个零点,求a的取值范围;
(2)若对任意x>0,恒有不等式f(x)≥1成立. ①求实数a的值;
②证明:x2ex>(x+2)lnx+2sinx.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现在,很多人都喜欢骑“共享单车”,但也有很多市民并不认可.为了调查人们对这种交通方式的认可度,某同学从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20名市民,得到了一个市民是否认可的样本,具体数据如下![]() 列联表:
列联表:
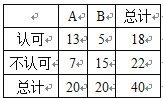
附:![]() ,
,![]() .
.

根据表中的数据,下列说法中,正确的是( )
A. 没有95% 以上的把握认为“是否认可与城市的拥堵情况有关”
B. 有99% 以上的把握认为“是否认可与城市的拥堵情况有关”
C. 可以在犯错误的概率不超过0.01的前提下认为“是否认可与城市的拥堵情况有关”
D. 可以在犯错误的概率不超过0.025的前提下认为“是否认可与城市的拥堵情况有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,AP=AB,平面PAB⊥平面ABC,∠ABC=90°,D,E分别为PB,BC的中点.
(1)求证:DE∥平面PAC;
(2)求证:DE⊥AD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com