
分析 通过对h(x)=f(2x+a)-2f(x)取绝对值符号,观察分段函数,分a<0、a>0、a=0三种情况讨论即可.
解答 解:设h(x)=f(2x+a)-2f(x),
则h(x)=|2x+a-a|-2|x-a|=2|x|-2|x-a|,
①当a<0时,去绝对值符号,得h(x)=$\left\{\begin{array}{l}{2a,}&{x≥0}\\{-4x+2a,}&{a<x<0}\\{-2a,}&{x≤a}\end{array}\right.$,
由|h(x)|≤2得|-4x+2a|≤2,
即$\frac{a-1}{2}$≤x≤$\frac{a+1}{2}$,
又已知关于x的不等式|f(2x+a)-2f(x)|≤2的解集{x|1≤x≤2},
所以$\left\{\begin{array}{l}{\frac{a-1}{2}=1}\\{\frac{a+1}{2}=2}\end{array}\right.$,
故a=3,这与a<0矛盾,故此时不满足题意;
②当a≥0时,去绝对值符号,得h(x)=$\left\{\begin{array}{l}{-2a,}&{x≤0}\\{4x-2a,}&{0<x<a}\\{2a,}&{x≥a}\end{array}\right.$,
由|h(x)|≤2得|4x-2a|≤2,
即$\frac{a-1}{2}$≤x≤$\frac{a+1}{2}$,
又已知关于x的不等式|f(2x+a)-2f(x)|≤2的解集{x|1≤x≤2},
所以$\left\{\begin{array}{l}{\frac{a-1}{2}=1}\\{\frac{a+1}{2}=2}\end{array}\right.$,
故a=3;
③当a=0时,易得不满足题意;
综上所述,a=3.
点评 本题考查解不等式,考查分类讨论的思想,注意解题方法的积累,属于中档题.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:填空题
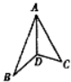 在正三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=$\frac{1}{2}$AB,这时二面角B-AD-C的大小为60°.
在正三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=$\frac{1}{2}$AB,这时二面角B-AD-C的大小为60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点,求证:
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com