
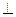 平面ABCD,AE=EB=BC=2,F为CE上的点,
平面ABCD,AE=EB=BC=2,F为CE上的点,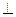 平面ACE.
平面ACE.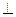 BE;
BE;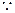 ABCD是矩形,
ABCD是矩形,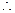 BC
BC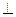 AB,
AB,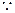 平面EAB
平面EAB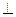 平面ABCD,
平面ABCD,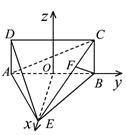
 平面ABCD=AB,BC
平面ABCD=AB,BC 平面ABCD,
平面ABCD, BC
BC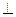 平面EAB,
平面EAB,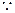 EA
EA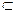 平面EAB,
平面EAB,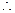 BC
BC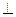 EA ,
EA ,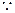 BF
BF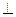 平面ACE,EA
平面ACE,EA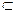 平面ACE,
平面ACE,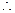 BF
BF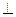 EA,
EA,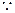 BC
BC  BF=B,BC
BF=B,BC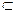 平面EBC,BF
平面EBC,BF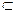 平面EBC,
平面EBC,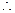 EA
EA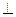 平面EBC ,
平面EBC ,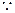 BE
BE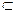 平面EBC,
平面EBC,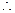 EA
EA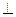 BE。
BE。 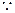 EA
EA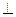 BE,
BE,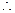 AB=
AB=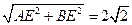
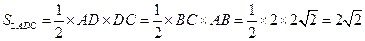 ,设O为AB的中点,连结EO
,设O为AB的中点,连结EO ,
,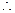 EO
EO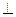 AB,
AB,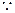 平面EAB
平面EAB 平面ABCD,
平面ABCD, EO
EO 平面ABCD,即EO为三棱锥E—ADC的高,且EO=
平面ABCD,即EO为三棱锥E—ADC的高,且EO=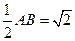 ,
,
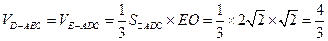 。
。 直线为
直线为 ,如图建立空间直角坐标系,则
,如图建立空间直角坐标系,则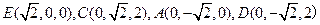 ,
,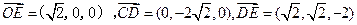 ,由(2)知
,由(2)知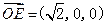 是平面ACD的一个法向量,设平面ECD的法向量为
是平面ACD的一个法向量,设平面ECD的法向量为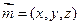 ,则
,则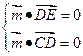 ,即
,即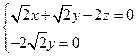 ,令
,令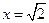 ,则
,则 ,所以
,所以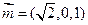 ,设二面角A—CD—E的平面角的大小为
,设二面角A—CD—E的平面角的大小为 ,由图得
,由图得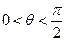 ,
,
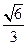 。
。

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
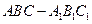 ,在某个空间直角坐标系中,
,在某个空间直角坐标系中, ,
,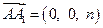 ,其中
,其中 、
、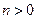

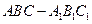 是正三棱柱;
是正三棱柱;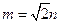 ,求直线
,求直线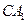 与平面
与平面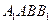 所成角的大小。
所成角的大小。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
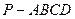 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 =2,
=2,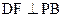 ,垂足为F。
,垂足为F。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 棱PA="PD" =
棱PA="PD" =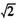 ,底面 ABCD为直角梯形,其中BC//AD,AB丄AD,AD=2AB=2BC=2,0为AD中点.
,底面 ABCD为直角梯形,其中BC//AD,AB丄AD,AD=2AB=2BC=2,0为AD中点.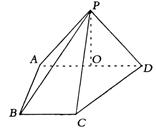
 PCD的距离.
PCD的距离.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,则倾斜后水槽中的水形成的几何体是
,则倾斜后水槽中的水形成的几何体是 ( )
( )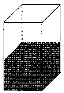
| A.棱柱 | B.棱台 | C.棱柱与棱锥 的组合体 的组合体 | D.不能确定 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
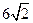 ,E为AD的中点(图一)。沿BE将△ABE折起,使二面角A—BE—C为直二面角(图二),且F为AC的中点。
,E为AD的中点(图一)。沿BE将△ABE折起,使二面角A—BE—C为直二面角(图二),且F为AC的中点。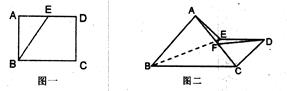
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com