
分析 (1)由诱导公式可化简即可得解.
(2)利用f(α)=-sinα,利用诱导公式,特殊角的三角函数值即可求值得解.
(3)由题意可得sinα=-$\frac{2\sqrt{6}}{5}$,由同角三角函数基本关系式可得cosα,进而利用诱导公式即可得解.
解答 解:(1)f(α)=$\frac{sin(\frac{3π}{2}-α)cos(\frac{π}{2}-α)tan(-α+π)}{sin(\frac{π}{2}+α)tan(2π-α)}$=$\frac{(-cosα)•(sinα)•(-tanα)}{(cosα)•(-tanα)}$=-sinα;
(2)f(α)=f(-$\frac{32}{3}$π)=-sin(-$\frac{32}{3}$π)=sin$\frac{32}{3}$π=sin$\frac{2π}{3}$=$\frac{\sqrt{3}}{2}$;
(3)∵f(α)=-sinα=$\frac{2\sqrt{6}}{5}$,
∴sinα=-$\frac{2\sqrt{6}}{5}$,
又α为第三象限角,
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\sqrt{1-(-\frac{2\sqrt{6}}{5})^{2}}$=-$\frac{1}{5}$,
∴cos(π+α)=-cosα=$\frac{1}{5}$.
点评 本题主要考查了诱导公式,特殊角的三角函数值,同角三角函数基本关系式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | g(x)的图象关于直线$x=\frac{π}{2}$对称 | B. | g(x)的图象关于点(π,0)对称 | ||
| C. | g(x)在$[0,\frac{π}{2}]$上递增 | D. | g(x)在[0,π]上递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
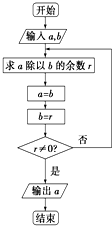 我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大的创举,这个伟大创举与古老的算法--“辗转相除法”实质一样,如图的程序框图源于“辗转相除法”.当输入a=6102,b=2016时,输出的a=( )
我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大的创举,这个伟大创举与古老的算法--“辗转相除法”实质一样,如图的程序框图源于“辗转相除法”.当输入a=6102,b=2016时,输出的a=( )| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{36}$ | B. | $\frac{4}{21}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{5}$,0),(-$\sqrt{5}$,0) | B. | (0,$\sqrt{5}$),(0,-$\sqrt{5}$) | C. | ($\frac{\sqrt{5}}{6}$,0),(-$\frac{\sqrt{5}}{6}$,0) | D. | (0,$\frac{\sqrt{5}}{6}$),(0,-$\frac{\sqrt{5}}{6}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com