
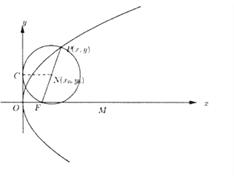
【题目】在直角坐标系![]() 中,
中, ![]() ,动点
,动点![]() 满足:以
满足:以![]() 为直径的圆与
为直径的圆与![]() 轴相切.
轴相切.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 交于
交于![]() 两点,当
两点,当![]() 与
与![]() 的面积之和取得最小值时,求直线
的面积之和取得最小值时,求直线![]() 的方程.
的方程.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)设点![]() ,圆心
,圆心![]() ,由圆与
,由圆与![]() 轴相切于点
轴相切于点![]() ,得|
,得| ![]() ,结合两点间的距离公式整理可得点P的轨迹方程为
,结合两点间的距离公式整理可得点P的轨迹方程为![]() ;
;
(2)(ⅰ)当直线l的斜率不存在时,方程为![]() ,可得
,可得![]() .
.
(ⅱ)当直线l的斜率存在时,设方程为![]() 联立直线方程与抛物线方程,可得关于
联立直线方程与抛物线方程,可得关于![]() 的一元二次方程,利用根与系数的关系可得
的一元二次方程,利用根与系数的关系可得![]()
再由![]() ,结合等号成立的条件求得
,结合等号成立的条件求得![]() 的值,进一步得到
的值,进一步得到![]() 值,则
值,则![]() 与
与![]() 的面积之和取得最小值时,直线
的面积之和取得最小值时,直线![]() 的方程可求
的方程可求
试题解析:
(1)设点![]() ,圆心
,圆心![]() ,
,
圆与![]() 轴相切于点
轴相切于点![]() ,则
,则![]() ,
,
所以![]() ,
,
又点![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
所以![]() ,整理得:
,整理得: ![]() .
.
所以点![]() 的轨迹方程为:
的轨迹方程为: ![]() .
.
(2)(ⅰ)当直线![]() 的斜率不存在时,方程为:
的斜率不存在时,方程为: ![]() ,
,
易得![]() .
.
(ⅱ)当直线![]() 的斜率存在时,设方程为:
的斜率存在时,设方程为: ![]() ,
, ![]() ,
, ![]() ,
,
由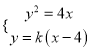 消去
消去![]() 并整理得:
并整理得: ![]() ,
,
所以![]() ,
, ![]() ,
,
所以![]()
![]() ,
,
当且仅当![]() 时等号成立,又
时等号成立,又![]() ,
,
所以![]() ,
, ![]() 或
或![]() ,
, ![]() ,
,
所以![]() ,解得:
,解得: ![]() ,
,
因为![]() ,所以当两个三角形的面积和最小时,
,所以当两个三角形的面积和最小时,
直线![]() 的方程为:
的方程为: ![]() .
.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理, ![]() 得到下表2:
得到下表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)通过(Ⅰ)中的方程,求出y关于x的回归方程;
(Ⅲ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中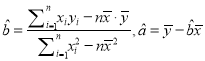 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“中华好诗词”节目的播出,掀起了全民诵读传统诗词经典的热潮.某社团为调查大学生对于“中华诗词”的喜好,从甲、乙两所大学各随机抽取了40名学生,记录他们每天学习“中华诗词”的时间,并整理得到如下频率分布直方图:

根据学生每天学习“中华诗词”的时间,可以将学生对于“中华诗词”的喜好程度分为三个等级 :
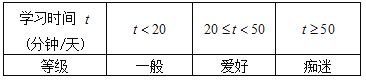
(Ⅰ)从甲大学中随机选出一名学生,试估计其“爱好”中华诗词的概率;
(Ⅱ)从两组“痴迷”的同学中随机选出2人,记![]() 为选出的两人中甲大学的人数,求
为选出的两人中甲大学的人数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(Ⅲ)试判断选出的这两组学生每天学习“中华诗词”时间的平均值![]() 与
与![]() 的大小,及方差
的大小,及方差![]() 与
与![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为坐标原点,动点
为坐标原点,动点![]() 在椭圆
在椭圆![]() 上,过
上,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 满足
满足![]() .(Ⅰ)求点
.(Ⅰ)求点![]() 的轨迹方程
的轨迹方程![]() ;
;
(Ⅱ)过![]() 的直线
的直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 两点,过
两点,过![]() 作与
作与![]() 垂直的直线
垂直的直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 两点,求证:
两点,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴不重合,
轴不重合, ![]() 交圆
交圆![]() 于
于![]() 两点,过
两点,过![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)证明![]() 为定值,并写出点
为定值,并写出点![]() 的轨迹方程;
的轨迹方程;
(2)设![]() ,过点
,过点![]() 作直线
作直线![]() ,交点
,交点![]() 的轨迹于
的轨迹于![]() 两点 (异于
两点 (异于![]() ),直线
),直线![]() 的斜率分别为
的斜率分别为![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
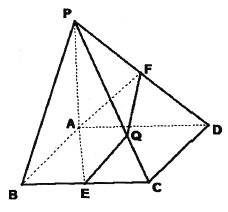
【题目】如图,在底面是菱形的四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 分别为
分别为![]() 的中点,设直线
的中点,设直线![]() 与平面
与平面![]() 交于点
交于点![]() .
.
(1)已知平面![]() 平面
平面![]() ,求证:
,求证: ![]() .
.
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com