Question

13．定义：若m-$\frac{1}{2}$＜x≤m+$\frac{1}{2}$（m为整数），则m叫做离实数x最近的整数，记作[x]，即[x]=m，若函数f（x）=x-[x
]与函数g（x）=ax²+bx的图象恰有1个公共点，则a，b的取值不可能是（　　）

• A． a=5，b=1
• B． a=4，b=-1
• C． a=-2，b=-1
• D． a=-4，b=1

Answer 1

分析 根据题意，先对函数化简，然后作出函数的图象，根据函数的图象可判断各个选项是否正确．

解答 解：令x=m+t，t∈（-$\frac{1}{2}$，$\frac{1}{2}$]，
∴f（x）=x-{x}=t∈（-$\frac{1}{2}$，$\frac{1}{2}$]，则函数f（x）=x-[x]的值域为（-$\frac{1}{2}$，$\frac{1}{2}$]，
又f（-x）=-x-[-x]=-x+[x]=-（x-[x]）=-f（x），
∴f（x）为奇函数．
图象如图：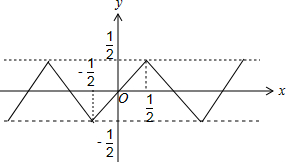

当a=-2，b=-1时，抛物线g（x）=-2x²-x的对称轴分成为x=$-\frac{1}{2}$，
而g（$-\frac{1}{2}$）=$-2×（-\frac{1}{2}）^{2}-（-\frac{1}{2}）=0$，图象与f（x）的图象有两个交点，与题意不符．
故选：C．

点评 本题为新定义题目，解题的关键是读懂定义内涵，尝试探究解决，属难题．