
已知函数f(x)=lnx+a ,其中a为大于零的常数.
,其中a为大于零的常数.
(1)若函数f(x)在区间[1,+∞)内单调递增,求实数a的取值范围.
(2)求证:对于任意的n∈N*,且n>1时,都有lnn> +
+ +…+
+…+ 恒成
恒成 立.
立.
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(三)(解析版) 题型:选择题
已知{an}为等差数列,其公差为-2,且a7是a3与a9的等比中项,Sn为{an}的前n项和,n∈N*,则S10的值为( )
A.-110 B.-90 C.90 D.110
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第四章平面向量、数系扩充与复数引入(解析版) 题型:选择题
下面是关于复数z= +
+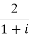 的四个命题:
的四个命题:
p1:|z|=2;p2:z2=4i;p3: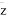 =2i;p4:z的虚部是0,其中的真命题为( )
=2i;p4:z的虚部是0,其中的真命题为( )
A.p1,p2 B.p1,p3 C.p2,p3 D.p3,p4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第十章 算法初步、统计、统计案例(解析版) 题型:填空题
(2014·天门模拟)在区间[0,4]内随机取两个数a,b,则使得函数f(x)=x2+ax+b2有零点的概率为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第十章 算法初步、统计、统计案例(解析版) 题型:选择题
(2014·武汉模拟)如图面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD投掷1000个点,落在矩形ABCD的非阴影部分中的点数为400个,试估计阴影部分的面积为( )

A.2.2 B.2.4
C.2.6 D.2.8
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第六章 不等式、推理与证明(解析版) 题型:填空题
对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义:f′′(x)是函数y=f(x)的导数f′(x)的导数,若方程f′′(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有′拐点′;任何一个三次函数都有对称中心,且‘拐点’就是对称中心”.请你将这一发现作为条件,则函数f(x)=x3-3x2+3x的对称中心为__________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第六章 不等式、推理与证明(解析版) 题型:选择题
(2013·随州模拟)变量x,y满足约束条件 则目标函数z=3|x|+|y-3|的取值范围是( )
则目标函数z=3|x|+|y-3|的取值范围是( )
A. B.
B. C.[-2,3] D.[1,6]
C.[-2,3] D.[1,6]
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第八章 平面解析几何(解析版) 题型:填空题
(2014·武汉模拟)圆(x-a)2+y2=1与双曲线x2-y2=1的渐近线相切,则a的值是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第二章 函数、导数及其应用(解析版) 题型:解答题
设函数f(x)=log3(9x)·log3(3x), ≤x≤9.
≤x≤9.
(1)若m=log3x,求m的取值范围.
(2)求f(x)的最值,并给出最值时对应的x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com