
【题目】已知函数![]() ,函数
,函数![]() 在点
在点![]() 处的切线斜率为0.
处的切线斜率为0.
(1)试用含有![]() 的式子表示
的式子表示![]() ,并讨论
,并讨论![]() 的单调性;
的单调性;
(2)对于函数![]() 图象上的不同两点
图象上的不同两点![]() ,
,![]() ,如果在函数
,如果在函数![]() 图象上存在点
图象上存在点![]() ,使得在点
,使得在点![]() 处的切线
处的切线![]() ,则称
,则称![]() 存在“跟随切线”.特别地,当
存在“跟随切线”.特别地,当![]() 时,又称
时,又称![]() 存在“中值跟随切线”.试问:函数
存在“中值跟随切线”.试问:函数![]() 上是否存在两点
上是否存在两点![]() 使得它存在“中值跟随切线”,若存在,求出
使得它存在“中值跟随切线”,若存在,求出![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
【答案】(1)![]() ,单调性见解析;(2)不存在,理由见解析
,单调性见解析;(2)不存在,理由见解析
【解析】
(1)由题意得![]() ,即可得
,即可得![]() ;求出函数
;求出函数![]() 的导数
的导数![]() ,再根据
,再根据![]() 、
、![]() 、
、![]() 、
、![]() 分类讨论,分别求出
分类讨论,分别求出![]() 、
、![]() 的解集即可得解;
的解集即可得解;
(2)假设满足条件的![]() 、
、![]() 存在,不妨设
存在,不妨设![]() ,
,![]() 且
且![]() ,由题意得
,由题意得![]() 可得
可得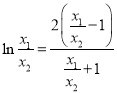 ,令
,令![]() (
(![]() ),构造函数
),构造函数![]() (
(![]() ),求导后证明
),求导后证明![]() 即可得解.
即可得解.
(1)由题可得函数![]() 的定义域为
的定义域为![]() 且
且![]() ,
,
由![]() ,整理得
,整理得![]() .
.
![]() .
.
(ⅰ)当![]() 时,易知
时,易知![]() ,
,![]() ,
,![]() 时
时![]() .
.
故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(ⅱ)当![]() 时,令
时,令![]() ,解得
,解得![]() 或
或![]() ,则
,则
①当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上恒成立,则
上恒成立,则![]() 在
在![]() 上递增.
上递增.
②当![]() ,即
,即![]() 时,当
时,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上单调递增,
上单调递增,![]() 单调递减,
单调递减,![]() 单调递增.
单调递增.
③当![]() ,即
,即![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上单调递增,
上单调递增,![]() 单调递减,
单调递减,![]() 单调递增.
单调递增.
综上,当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 单调递减.
单调递减.
当![]() 时,
时,![]() 在
在![]() 及
及![]() 上单调递增;
上单调递增;![]() 在
在![]() 上单调递减.
上单调递减.
当![]() 时,
时,![]() 在
在![]() 上递增.
上递增.
当![]() 时,
时,![]() 在
在![]() 及
及![]() 上单调递增;
上单调递增;![]() 在
在![]() 上递减.
上递减.
(2)满足条件的![]() 、
、![]() 不存在,理由如下:
不存在,理由如下:
假设满足条件的![]() 、
、![]() 存在,不妨设
存在,不妨设![]() ,
,![]() 且
且![]() ,
,
则![]() ,
,
又![]() ,
,
由题可知![]() ,整理可得:
,整理可得: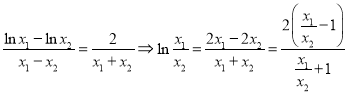 ,
,
令![]() (
(![]() ),构造函数
),构造函数![]() (
(![]() ).
).
则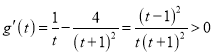 ,
,
所以![]() 在
在![]() 上单调递增,从而
上单调递增,从而![]() ,
,
所以方程![]() 无解,即
无解,即![]() 无解.
无解.
综上,满足条件的A、B不存在.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案科目:高中数学 来源: 题型:
【题目】超级病菌是一种耐药性细菌,产生超级细菌的主要原因是用于抵抗细菌侵蚀的药物越来越多,但是由于滥用抗生素的现象不断的发生,很多致病菌也对相应的抗生素产生了耐药性,更可怕的是,抗生素药物对它起不到什么作用,病人会因为感染而引起可怕的炎症,高烧、痉挛、昏迷直到最后死亡.某药物研究所为筛查某种超级细菌,需要检验血液是否为阳性,现有n(![]() )份血液样本,每个样本取到的可能性均等,有以下两种检验方式:
)份血液样本,每个样本取到的可能性均等,有以下两种检验方式:
(1)逐份检验,则需要检验n次;
(2)混合检验,将其中k(![]() 且
且![]() )份血液样本分别取样混合在一起检验,若检验结果为阴性,这k份的血液全为阴性,因而这k份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份再逐份检验,此时这k份血液的检验次数总共为
)份血液样本分别取样混合在一起检验,若检验结果为阴性,这k份的血液全为阴性,因而这k份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份再逐份检验,此时这k份血液的检验次数总共为![]() 次,假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为p(
次,假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为p(![]() ).
).
(1)假设有5份血液样本,其中只有2份样本为阳性,若采用逐份检验方式,求恰好经过2次检验就能把阳性样本全部检验出来的概率;
(2)现取其中k(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
(i)试运用概率统计的知识,若![]() ,试求p关于k的函数关系式
,试求p关于k的函数关系式![]() ;
;
(ii)若![]() ,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求k的最大值.
,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求k的最大值.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aex,g(x)=lnx-lna,其中a为常数,且曲线y=f(x)在其与y轴的交点处的切线记为l1,曲线y=g(x)在其与x轴的交点处的切线记为l2,且l1∥l2.
(1)求l1,l2之间的距离;
(2)若存在x使不等式![]() 成立,求实数m的取值范围;
成立,求实数m的取值范围;
(3)对于函数f(x)和g(x)的公共定义域中的任意实数x0,称|f(x0)-g(x0)|的值为两函数在x0处的偏差.求证:函数f(x)和g(x)在其公共定义域内的所有偏差都大于2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉所著的《详解九章算术》一书中,用图①的数表列出了一些正整数在三角形中的一种几何排列,俗称“杨辉三角形”,该数表的规律是每行首尾数字均为![]() ,从第三行开始,其余的数字是它“上方”左右两个数字之和。现将杨辉三角形中的奇数换成
,从第三行开始,其余的数字是它“上方”左右两个数字之和。现将杨辉三角形中的奇数换成![]() ,偶数换成
,偶数换成![]() ,得到图②所示的由数字
,得到图②所示的由数字![]() 和
和![]() 组成的三角形数表,由上往下数,记第
组成的三角形数表,由上往下数,记第![]() 行各数字的和为
行各数字的和为![]() ,如
,如![]() ,则
,则![]() ____________
____________
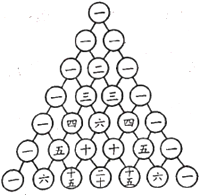

① ②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 设椭圆![]() 的左焦点为
的左焦点为![]() ,左顶点为
,左顶点为![]() ,顶点为B.已知
,顶点为B.已知![]() (
(![]() 为原点).
为原点).
(Ⅰ)求椭圆的离心率;
(Ⅱ)设经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆在
与椭圆在![]() 轴上方的交点为
轴上方的交点为![]() ,圆
,圆![]() 同时与
同时与![]() 轴和直线
轴和直线![]() 相切,圆心
相切,圆心![]() 在直线
在直线![]() 上,且
上,且![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生活中人们常用“通五经贯六艺”形容一个人才识技艺过人,这里的“六艺”其实源于中国周朝的贵族教育体系,具体包括“礼、乐、射、御、书、数”.为弘扬中国传统文化,某校在周末学生业余兴趣活动中开展了“六艺”知识讲座,每艺安排一节,连排六节,则满足“数”必须排在前两节,“礼”和“乐”必须分开安排的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四面体![]() 底面的中心为
底面的中心为![]() ,
,![]() 的重心为
的重心为![]() .
.![]() 是
是![]() 内部一动点(包括边界),满足
内部一动点(包括边界),满足![]() ,
,![]() ,
,![]() 不共线且点
不共线且点![]() 到点
到点![]() 的距离与到平面
的距离与到平面![]() 的距离相等.
的距离相等.
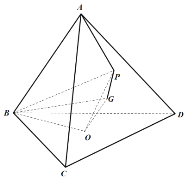
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求四面体
,求四面体![]() 体积的最大值.
体积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com