
���� ��������f��x����ͼ����O��������ֱ�����������ӽ���x��0ʱ������y=$\sqrt{{x}^{2}+1}$��ֱ��y=k1x���ӽ������ǽ����ߣ����k1=1��x��0ʱ�����߿ɻ�Ϊx2+��y-2��2=1��x��0����Բ�ĵ�ֱ�ߵľ���Ϊ$\frac{2}{\sqrt{{{k}_{2}}^{2}+1}}$=1����k2=-$\sqrt{3}$��������ֱ�ߵļнǹ�ʽ���ɵõ�����ġ�ȷ��ǡ���
��� 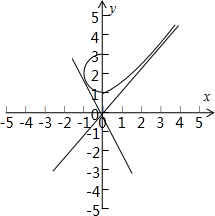 �⣺��������f��x����ͼ����O��������ֱ�����������ӽ��������ǵķ��̷ֱ�Ϊy=k1x��y=k2x��
�⣺��������f��x����ͼ����O��������ֱ�����������ӽ��������ǵķ��̷ֱ�Ϊy=k1x��y=k2x��
��x��0ʱ������y=$\sqrt{{x}^{2}+1}$��ֱ��y=k1x���ӽ�����Ϊ˫���ߵĽ����ߣ���k1=1��
��x��0ʱ�����߿ɻ�Ϊx2+��y-2��2=1��x��0����Բ�ĵ�ֱ�ߵľ���Ϊ$\frac{2}{\sqrt{{{k}_{2}}^{2}+1}}$=1����k2=-$\sqrt{3}$��
����ֱ�ߵļнǹ�ʽ�ã�tan��=|$\frac{1+\sqrt{3}}{1-\sqrt{3}}$|=2+$\sqrt{3}$��
������C����ڵ�O�ġ�ȷ��ǡ�Ϊ$\frac{5��}{12}$��
�ʴ�Ϊ��$\frac{5��}{12}$��
���� ���⿼���¶��塰ȷ��ǡ���Ӧ�ã�����ֱ����Բ��λ�ù�ϵ��˫���ߵ����ʣ������ߣ������е��⣮


 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $x=-\frac{��}{12}$ | B�� | $x=\frac{��}{12}$ | C�� | $x=\frac{��}{3}$ | D�� | $x=\frac{2��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{3}^{6}-1}{2}$ | B�� | $\frac{{3}^{6}+1}{2}$ | C�� | $\frac{{3}^{6}+2}{2}$ | D�� | $\frac{{3}^{6}-2}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | $\frac{1}{2}$ | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com