
分析 由三角函数的定义求出sinα的值判断①;根据题意,画出单位圆以及α,β为第二象限的角的三角函数线,根据三角函数线得到tanα<tanβ判断②;利用二倍角的正弦判断③;把已知等式两边平方可得sinx<0且cosx<0,x为第三象限角,得tanx>0判断④;直接求出x=-$\frac{π}{3}$时的函数y=3cos(2x-$\frac{π}{3}$)+1的函数值判断⑤.
解答 解:①若点P(a,2a)(a≠0)为角α终边上一点,则|OP|=$\sqrt{5}|a|$,
当a>0时,sinα=$\frac{2a}{\sqrt{5}a}$=$\frac{2\sqrt{5}}{5}$,当a<0时,sinα=$\frac{2a}{-\sqrt{5}a}=-\frac{2\sqrt{5}}{5}$,故①错误;
②若sinα>sinβ,且α,β均为第二象限角,三角函数线如图,
则tanα<tanβ,故②正确;
③若θ是第二象限角,则sin$\frac{θ}{2}$cos$\frac{θ}{2}$=$\frac{1}{2}sinθ$>0,故③正确;
④若sinx+cosx=-$\frac{7}{5}$,得1+2sinxcosx=$\frac{49}{25}$,即sinxcosx=$\frac{12}{25}$,说明sinx<0且cosx<0,x为第三象限角,则tanx>0,故④错误;
⑤∵3cos[2×(-$\frac{π}{3}$)-$\frac{π}{3}$]=3cos(-π)=-3,∴直线x=-$\frac{π}{3}$是函数y=3cos(2x-$\frac{π}{3}$)+1的图象的一条对称轴,故⑤正确.
∴正确命题的序号是②③⑤.
故答案为:②③⑤.
点评 本题考查命题的真假判断与应用,考查了三角函数的图象和性质,是中档题.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:解答题
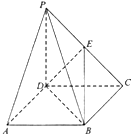 在如图所示的四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,且PD=CD=2,点E为PC的中点,连接DE,BD,BE.
在如图所示的四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,且PD=CD=2,点E为PC的中点,连接DE,BD,BE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=$\frac{1}{2}$,A>$\frac{3}{2}$ | B. | a=$\frac{1}{2}$,A≤$\frac{3}{2}$ | C. | a=1,A≥1 | D. | a=1,A≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
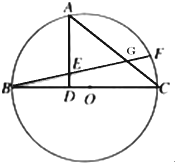 如图,BC是圆O的直径,点F在弧$\widehat{BC}$上,点A为弧$\widehat{BF}$的中点,作AD⊥BC于点D,BF与AD交于点E,BF与AC交于点G.
如图,BC是圆O的直径,点F在弧$\widehat{BC}$上,点A为弧$\widehat{BF}$的中点,作AD⊥BC于点D,BF与AD交于点E,BF与AC交于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com