
分析 (1)利用双曲线$\frac{x^2}{m}$+$\frac{y^2}{m-1}$=1,焦点在x轴上,可得$\left\{\begin{array}{l}{m>0}\\{m-1<0}\end{array}\right.$,即可求m的范围;
(2)求出倾角是45°的直线L的方程为y=x-1,代入双曲线方程,求出A的坐标,即可求原点O到A点的距离.
解答 解:(1)∵双曲线$\frac{x^2}{m}$+$\frac{y^2}{m-1}$=1,焦点在x轴上,
∴$\left\{\begin{array}{l}{m>0}\\{m-1<0}\end{array}\right.$,∴0<m<1;
(2)∵双曲线离心率是$\sqrt{2}$,∴m=1-m,∴m=$\frac{1}{2}$.
∴c=$\sqrt{\frac{1}{2}+\frac{1}{2}}$=1,
∴倾角是45°的直线L的方程为y=x-1,
代入双曲线方程,可得x=$\frac{3}{2}$,∴A($\frac{3}{2}$,±$\frac{\sqrt{7}}{2}$),
∴原点O到A点的距离是$\sqrt{\frac{9}{4}+\frac{7}{4}}$=2.
点评 本题考查双曲线的方程与性质,考查直线与双曲线的位置关系,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
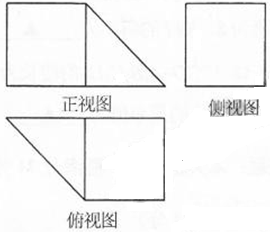 一个体积为8cm3的几何体的三视图如图所示(单位:cm),其中正视图和俯视图是一个等腰直角三角形和一个正方形,侧视图是一个正方形,则这个几何体的表面积是( )
一个体积为8cm3的几何体的三视图如图所示(单位:cm),其中正视图和俯视图是一个等腰直角三角形和一个正方形,侧视图是一个正方形,则这个几何体的表面积是( )| A. | $8+8\sqrt{2}\;c{m^2}$ | B. | $12+8\sqrt{2}\;c{m^2}$ | C. | $16+8\sqrt{2}\;c{m^2}$ | D. | $20+8\sqrt{2}\;c{m^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A,B,C,H四个小朋友在草坪上游戏,根据游戏规则,A,B,C三人围成一个三角形,B,H,C三人共线,H在B,C两人之间.B,C两人相距10m,A,H两人相距hm,AH与BC垂直.
如图,A,B,C,H四个小朋友在草坪上游戏,根据游戏规则,A,B,C三人围成一个三角形,B,H,C三人共线,H在B,C两人之间.B,C两人相距10m,A,H两人相距hm,AH与BC垂直.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解2015-2016学年高一学生的体能情况,某校随机抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频率直方图.如图所示,已知次数在[100,110)间的频数为7,次数在110以下(不含110)视为不达标,次数在[110,130)视为达标,次数在130以上视为有优秀.
为了解2015-2016学年高一学生的体能情况,某校随机抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频率直方图.如图所示,已知次数在[100,110)间的频数为7,次数在110以下(不含110)视为不达标,次数在[110,130)视为达标,次数在130以上视为有优秀.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 44 | B. | 43 | C. | 42 | D. | 41 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com