
分析 由题意:设母线l,底面半径为r,则圆锥的高h=$\sqrt{{l}^{2}{-r}^{2}}$,那么侧面积S侧=πrl,过轴的截面面积S截=r•h,它们比为2π,即可得到半径与母线的比.
解答 解:由题意:圆锥的侧面面积与过轴的截面面积之比为2π;
设母线l,底面半径为r,则圆锥的高h=$\sqrt{{l}^{2}{-r}^{2}}$,
那么侧面积S侧=πrl,
过轴的截面面积S截=r•h,
∴$\frac{πrl}{r•\sqrt{{l}^{2}-{r}^{2}}}=2π$
解得:2r=$\sqrt{3}l$
所以:半径与母线的比为:$\frac{\sqrt{3}}{2}$
故答案为$\frac{\sqrt{3}}{2}$.
点评 本题考查了圆锥的侧面面积的计算和截面面积的计算.考查对公式的熟悉程度.属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下命题:“尽有委米依坦内角,下周八尺,高五尺,圆周率约为三,问:积为几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,已知圆周率约为3,问米堆的体积为多少?”( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下命题:“尽有委米依坦内角,下周八尺,高五尺,圆周率约为三,问:积为几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,已知圆周率约为3,问米堆的体积为多少?”( )| A. | $\frac{4096}{9}$ | B. | $\frac{1280}{9}$ | C. | $\frac{320}{9}$ | D. | $\frac{256}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
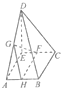 如图所示,四棱锥D-ABCE中,底面ABCE是矩形,G,F分别为AD,CE的中点,DE⊥AE,DE⊥EC.
如图所示,四棱锥D-ABCE中,底面ABCE是矩形,G,F分别为AD,CE的中点,DE⊥AE,DE⊥EC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{7}{2}$ | C. | $\frac{15}{4}$ | D. | $\frac{15}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com