
分析 (1)把条件中所给的既有角又有边的等式利用正弦定理变化成只有角的形式,整理逆用两角和的正弦公式,根据三角形内角的关系,得到结果.
(2)利用余弦定理写成关于角A的表示式,整理出两个边的积的范围,表示出三角形的面积,得到面积的最大值.
解答 解:(1)因为$\frac{2c-b}{a}=\frac{cosB}{cosA}$,所以(2c-b)cosA=acosB由正弦定理,
得(2sinC-sinB)cosA=sinAsinB,整理得2sinCcosA-sinBcosA=sinAcosB
所以2sinC-cosA=sin(A+B)=sinC
在△ABC中,sinC≠0,所以$cosA=\frac{1}{2},∠A=\frac{π}{3}$
(2)由余弦定理cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{1}{2}$,a=2$\sqrt{5}$.
∴b2+c2-20=bc≥2bc-20
∴bc≤20,当且仅当b=c时取“=”.
∴三角形的面积S=$\frac{1}{2}$bcsinA≤5$\sqrt{3}$.
∴三角形面积的最大值为5$\sqrt{3}$
点评 本题考查正弦定理和余弦定理,本题解题的关键是角和边的灵活互化,两个定理的灵活应用和两角和的公式的正用和逆用.


科目:高中数学 来源: 题型:解答题
 曲线C的方程为 $\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$(a>b>0),曲线经过点$(\frac{3}{2},1)$,曲线的离心率为$\frac{1}{2}$.
曲线C的方程为 $\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$(a>b>0),曲线经过点$(\frac{3}{2},1)$,曲线的离心率为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
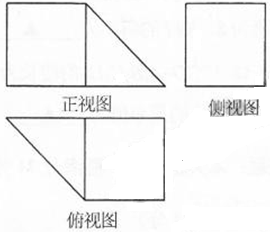 一个体积为8cm3的几何体的三视图如图所示(单位:cm),其中正视图和俯视图是一个等腰直角三角形和一个正方形,侧视图是一个正方形,则这个几何体的表面积是( )
一个体积为8cm3的几何体的三视图如图所示(单位:cm),其中正视图和俯视图是一个等腰直角三角形和一个正方形,侧视图是一个正方形,则这个几何体的表面积是( )| A. | $8+8\sqrt{2}\;c{m^2}$ | B. | $12+8\sqrt{2}\;c{m^2}$ | C. | $16+8\sqrt{2}\;c{m^2}$ | D. | $20+8\sqrt{2}\;c{m^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 44 | B. | 43 | C. | 42 | D. | 41 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com