
分析 (1)由题意,代入可得求a2、a3的值;
(2)由数列{an}中,a1=1,an+1=$\frac{a_n}{{{a_n}+4}}$可得{$\frac{1}{{a}_{n}}$+$\frac{1}{3}$}是首项为$\frac{4}{3}$,公比为4的等比数列,即可得出{an}的通项公式an;
(3)由(2)可知:bn,利用“错位相减法”即可得出Tn,利用不等式2n-1λ<2n-1Tn+$\frac{3n}{2}$对一切n∈N*恒成立,求λ的取值范围.
解答 解:(1)由题意,代入可得a2=$\frac{1}{5}$,a3=$\frac{2}{21}$;
(2)∵an+1=$\frac{a_n}{{{a_n}+4}}$,
∴$\frac{1}{{{a_{n+1}}}}=\frac{{{a_n}+4}}{a_n}=\frac{4}{a_n}+1$,
∴$\frac{1}{{{a_{n+1}}}}+\frac{1}{3}=4({\frac{1}{a_n}+\frac{1}{3}})\\∴数列\left\{{\frac{1}{a_n}+\frac{1}{3}}\right\}是以\frac{4}{3}为首项,4为公比的等比数列\\∴\frac{1}{a_n}+\frac{1}{3}=\frac{4^n}{3}∴{a_n}=\frac{3}{{{4^n}-1}}({(7分)})\\(3)代入{a_n}可得{b_n}=\frac{3n}{2^n},由错位相减法可得{T_n}=6-\frac{6+3n}{2^n}\\∵{2^{n-1}}λ<{2^{n-1}}{T_n}+\frac{3}{2}n,代入分离可得λ=6-\frac{6}{2^n}\\ 由函数的单调性可得关于n的函数单调递增\\∴当n=1时,函数有最小值3$,
∴{$\frac{1}{{a}_{n}}$+$\frac{1}{3}$}是首项为$\frac{4}{3}$,公比为4的等比数列,
∴$\frac{1}{{a}_{n}}$+$\frac{1}{3}$=$\frac{{4}^{n}}{3}$,
∴$\frac{1}{{a}_{n}}$=$\frac{{4}^{n}}{3}$-$\frac{1}{3}$,
∴an=$\frac{3}{{4}^{n}-1}$;
(3)bn=(4n-1)•$\frac{n}{2^n}$•an=$\frac{3n}{{2}^{n}}$,
Tn=3($\frac{1}{2}$+$\frac{2}{{2}^{2}}$+…+$\frac{n}{{2}^{n}}$),
∴$\frac{1}{2}$Tn=3($\frac{1}{{2}^{2}}+\frac{2}{{2}^{3}}$+…+$\frac{n}{{2}^{n+1}}$),
两式相减得$\frac{1}{2}$Tn=3($\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$-$\frac{n}{{2}^{n+1}}$)=3(1-$\frac{1}{{2}^{n}}$-$\frac{n}{{2}^{n+1}}$),
∴2n-1Tn=3(2n-1-$\frac{n}{2}$),
∵不等式2n-1λ<2n-1Tn+$\frac{3n}{2}$对一切n∈N*恒成立,
∴2n-1λ<3(2n-1),
∴λ<3(2-$\frac{1}{{2}^{n-1}}$),∴λ<3.
点评 熟练掌握等比数列的通项公式和前n项和公式、“错位相减法”等是解题的关键.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{4}{3}$] | B. | [3,+∞) | C. | [-2$\sqrt{2}$,2$\sqrt{2}$] | D. | [-3,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\frac{|x|}{x}$是奇函数 | B. | f(x)=x2,x∈(-3,3]是偶函数 | ||
| C. | f(x)=(x-3)2是非奇非偶函数 | D. | y=x4+x2是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,4} | B. | {-1,-4} | C. | {(-1,4)} | D. | {(-1,-4)} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
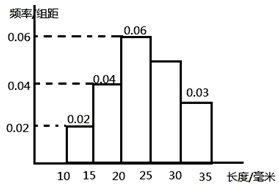 对一批产品的长度(单位:mm)进行抽样检测,如图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在[15,20)和[25,30)上的为二等品,在[10,15)和[30,35)上的为三等品;
对一批产品的长度(单位:mm)进行抽样检测,如图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在[15,20)和[25,30)上的为二等品,在[10,15)和[30,35)上的为三等品;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
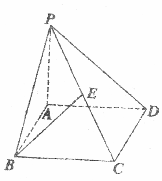 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内,有BE⊥PC于E,且BE=$\frac{{\sqrt{6}}}{3}$a.
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内,有BE⊥PC于E,且BE=$\frac{{\sqrt{6}}}{3}$a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com