
分析 (1)利用待定系数法求出△ABC的外接圆方程;
(2)定义代入法求线段MN的中点P的轨迹方程.
解答 解:(1)设△ABC的外接圆方程为 (x-a)2+(y-b)2=r2,
把A(0,1),B(2,1),C(3,4)代入圆的方程得,
$\left\{\begin{array}{l}{a^2}+{({b-1})^2}={r^2}\\{({a-2})^2}+{({b-1})^2}={r^2}\\{({a-3})^2}+{({b-4})^2}={r^2}\end{array}\right.$解此方程组,得$\left\{\begin{array}{l}a=1\\ b=3\\{r^2}=5\end{array}\right.$,
∴△ABC的外接圆方程是(x-1)2+(y-3)2=5.
(2)设点P(x,y),点M(x0,y0),
∵点P是MN的中点,∴$\left\{\begin{array}{l}x=\frac{{{x_0}+6}}{2}\\ y=\frac{{{y_0}+2}}{2}\end{array}\right.$,
于是有$\left\{\begin{array}{l}{x_0}=2x-6\\{y_0}=2y-2\end{array}\right.$,
∵点M在(x-1)2+(y-3)2=5的圆上运动,∴${({{x_0}-1})^2}+{({{y_0}-3})^2}=5$,
即∴(2x-6-1)2+(2y-2-3)2=5,整理得${({x-\frac{7}{2}})^2}+{({y-\frac{5}{2}})^2}=\frac{5}{4}$,
所以,点P的轨迹是以$({\frac{7}{2},\frac{5}{2}})$为圆心,半径长是$\frac{{\sqrt{5}}}{2}$的圆.
点评 本题考查轨迹方程,考查待定系数法、代入法的运用,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A={-1,0,1},B={0,1},f:A中的数平方 | B. | A={0,1},B={-1,0,1},f:A中的数开方 | ||
| C. | A=Z,B=Q,f:A中的数取倒数 | D. | A=R,B={正实数},f:A中的数取绝对值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 5 | C. | 4 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
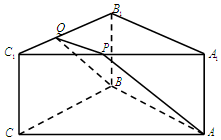 如图,ABC-A1B1C1是底面边长为2,高为$\frac{\sqrt{3}}{2}$的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).
如图,ABC-A1B1C1是底面边长为2,高为$\frac{\sqrt{3}}{2}$的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20不是这个数列中的项 | B. | 只有第5项是20 | ||
| C. | 只有第9项是20 | D. | 这个数列第5项、第9项都是20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com